Ref.

Visual explanations from spiking neural networks using inter‑spike intervals

Main Contents

本文提出脉冲激活图（Spike Activation Map, SAM）, 无需反向传播或依赖梯度即可获得“视觉解释”. 这与Grad-CAM不同（通过反向传播计算梯度来量化浅层到深层神经元对目标类别预测的贡献）

我们利用了这样一种生物学观察：短脉冲间隔（ISI）的脉冲在神经系统中包含更多信息，因为这些脉冲更可能通过提高神经元的膜电位来引发突触后脉冲。针对SNN所做出的预测，SAM为网络中的每个神经元计算一个神经元贡献分数（Neuronal Contribution Score, NCS）。NCS分数定义为先前脉冲的时间脉冲贡献分数（Temporal Spike Contribution Score, TSCS）的总和，并使用指数核函数计算。

对于在短时间窗口内多次脉冲的神经元，TSCS较高；相反，对于在较长时间内发放脉冲的神经元，TSCS较低。

Results Comparison

SNN 定制的 Grad-CAM(SNN‑crafted Grad‑CAM)

仿照Grad-CAM，计算跨所有时间步的 SNN 定制 Grad-CAM 热图量化每个通道的贡献：

$\alpha^{c,k}=\frac{1}{N}\sum_{i}\sum_{j}\sum_{t}\frac{\partial y^{c}}{\partial A_{i,j,i}^{k,c}}$

其中， $N$ 是归一化因子, $A_{i,j,t}^{k}$ 是第 $k$ 通道在时间步 $t$ 的脉冲激活值

$G_{i,j,t}^{c}=\operatorname*{max}\left(0,\sum_{k}\alpha_{t}^{c,k}A_{i,j,t}^{k}\right)$

需要提及的是，我们将静态图像转换为多时间步的脉冲序列（详见泊松编码）

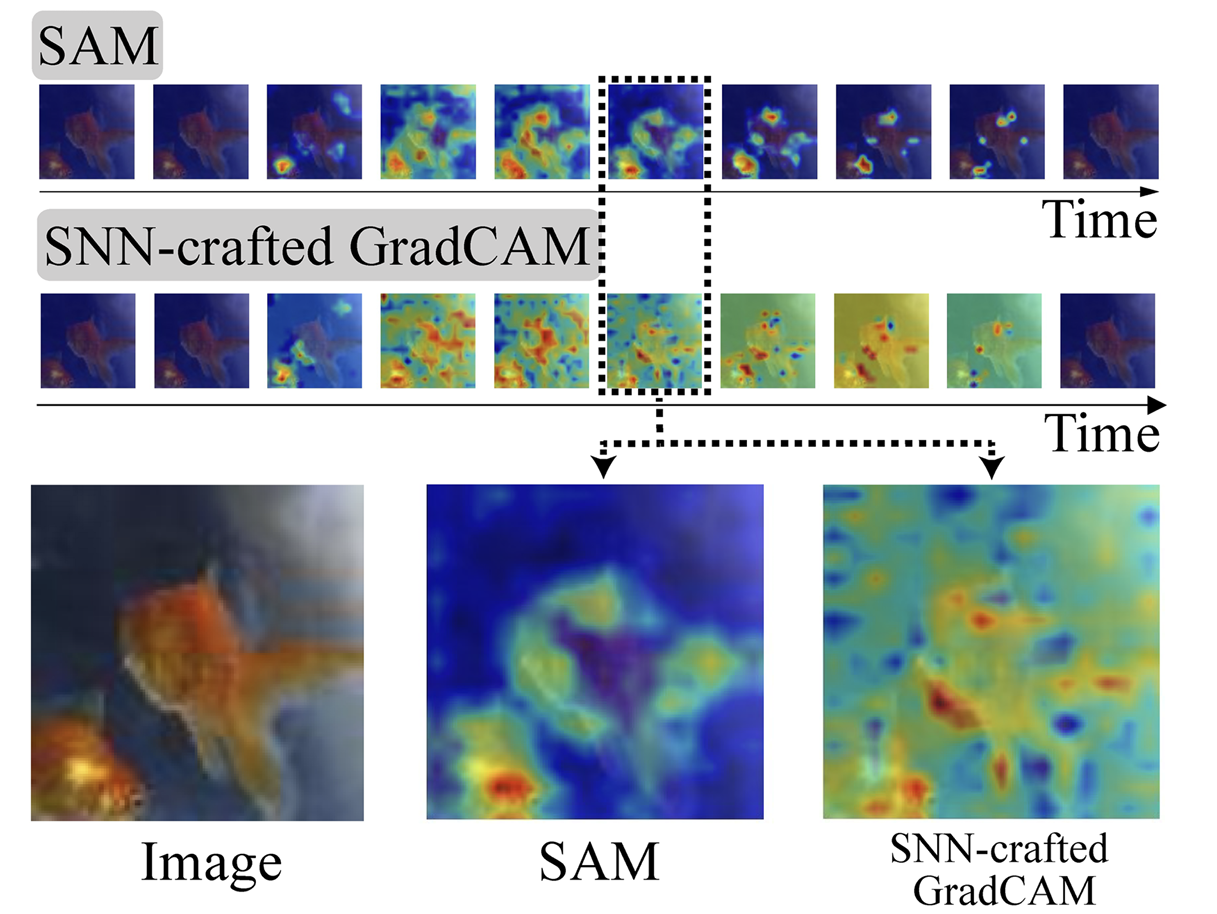
heatmap smoothing effect of SNN-Crafted-CAM

SNN-Crafted-CAM 存在一种被称为热图平滑效应的问题，这是由于近似的反向梯度函数导致的。

为了从量化角度验证“热图平滑效应”，我们计算了热图的像素级方差。因此，包含非区分信息（即类似像素值）的热图应该具有较低的方差。如图 2b 所示，与我们提出的 SAM（将在下一部分讨论）相比，SNN 定制 Grad-CAM 显示出较低的方差。

脉冲激活图（Spike Activation Map, SAM）

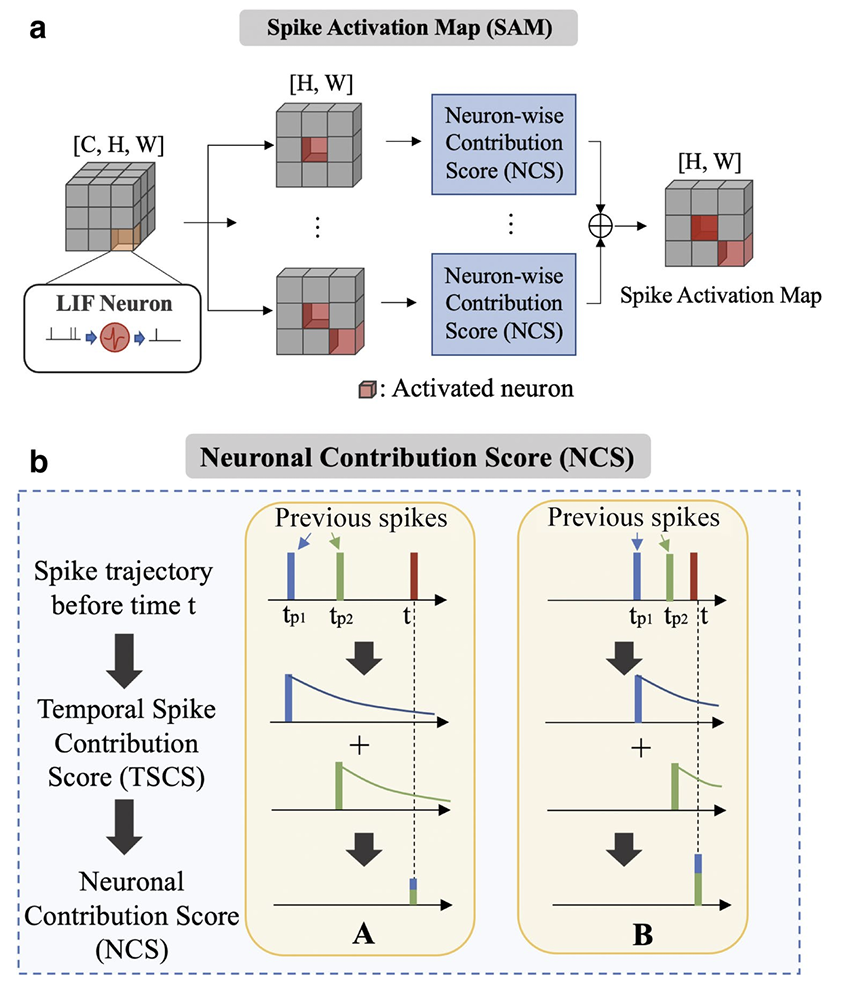
SAM 仅使用前向传播中的脉冲活动来计算热图。因此，这种可视化不仅针对特定类别，还可以高亮显示网络在任何给定图像上的关注区域。令人惊讶的是，我们观察到即使没有任何真实标签，SAM 也能生成有意义的可视化。用数学表述为（从所有因果时间步推断某个时刻下的脉冲贡献值）

$M_{t}\,\longleftarrow\,f\big(S_{0},S_{1},\cdot\cdot\cdot,\ S_{t-1}\big),$

首先我们定义时间脉冲贡献分数（TSCS）. TSCS 评估了时间 $t`$ 的先前脉冲相对于当前时间 $t$ 的贡献。很自然地，先前脉冲的贡献会随着时间的推移逐渐减小。因此，TSCS 值可以表述为：

$T(t,t^{\prime})=\exp(-\gamma|t-t^{\prime}|),$

其中， $\gamma$ 是控制指数核函数陡峭程度的超参数.

为了考虑多个先前脉冲，我们定义一个集合 $P_{ij}^{k}$ , 包含了神经元在位置 $(i,j)$ 和通道 $k$ 的先前发放时间。对每个 $P_{ij}^{k}$ 的先前脉冲TCDS求和得到每个神经元的贡献分数(NCS), $N_{ij,t}^{k}$

$N_{i j,t}^{k}=\sum_{t^{\prime}\in P_{i j}^{k}}T(t,t^{\prime}).$

如果一个神经元在短时间间隔内频繁发放脉冲，它的 NCS 值就会很高，反之亦然。最后，我们通过将脉冲发放值 $S_{ij}^{t}$ 与NCS值相乘，并对所有通道 $k$ 求和来计算时间步 $t$ 和位置 $(i,j)$ 的SAM值 $M_{ij,t}$

${M}_{i j,t}=\sum_{k}{N}_{i j,t}^{k}S_{i j,t}.$

Overall Structure of SAM

这个和膜电位的贡献还是有区别的，膜电位放完电之后会归零，而这个方法相当于不归零，且能够以一种稳定有效的方式发放脉冲并累计其贡献值。

结果分析

请注意，SAM 不需要任何类别标签，而 Grad-CAM 使用真实标签来生成热图。有趣的是，从 SAM 获取的跨不同时间步的热图在 SNN 上的结果与 ANN 上的 Grad-CAM 相似。SAM 突出了感兴趣的区域，并以区分性方式呈现。这支持了我们关于 SAM 是一种有效的 SNN 可视化工具的论断。此外，结果表明 ISI 和时间动态可以为深层 SNN 提供可解释性。

一直以来，人们假设 SNN 像 ANN 一样，随着层的加深，从通用特征到特定特征逐渐学习。首次，我们通过可视化 SNN 的中间层解释来支持这一假设。有趣的是，基于替代梯度学习的 SAM 可视化（图4c）显示SNN 的浅层代表低级结构，而深层关注语义信息。 例如，第4层高亮显示了狮子的边缘或斑点（如眼睛和鼻子），而第8层高亮显示了狮子的完整脸部。更多的可视化结果可见附录图2-7。

消融实验的理解

Localization error at layer 4 (top row), layer 6 (middle row), and layer 8 (bottom row) with respect to hyperparameter γ

$E = \operatorname*{min}_{t} \left\{ \frac{1}{N} \sum_{i,j} G_{ij} \log(M_{ij,t}) + (1 - G_{ij}) \log(1 - M_{ij,t}) \right\}$

式中， $E$ 为定位误差, $N$ 为归一化因子， $G_{ij}$ 为参考Grad-CAM图的像素值, $M_{ij,t}$ 为SAM在时间步t的像素值。

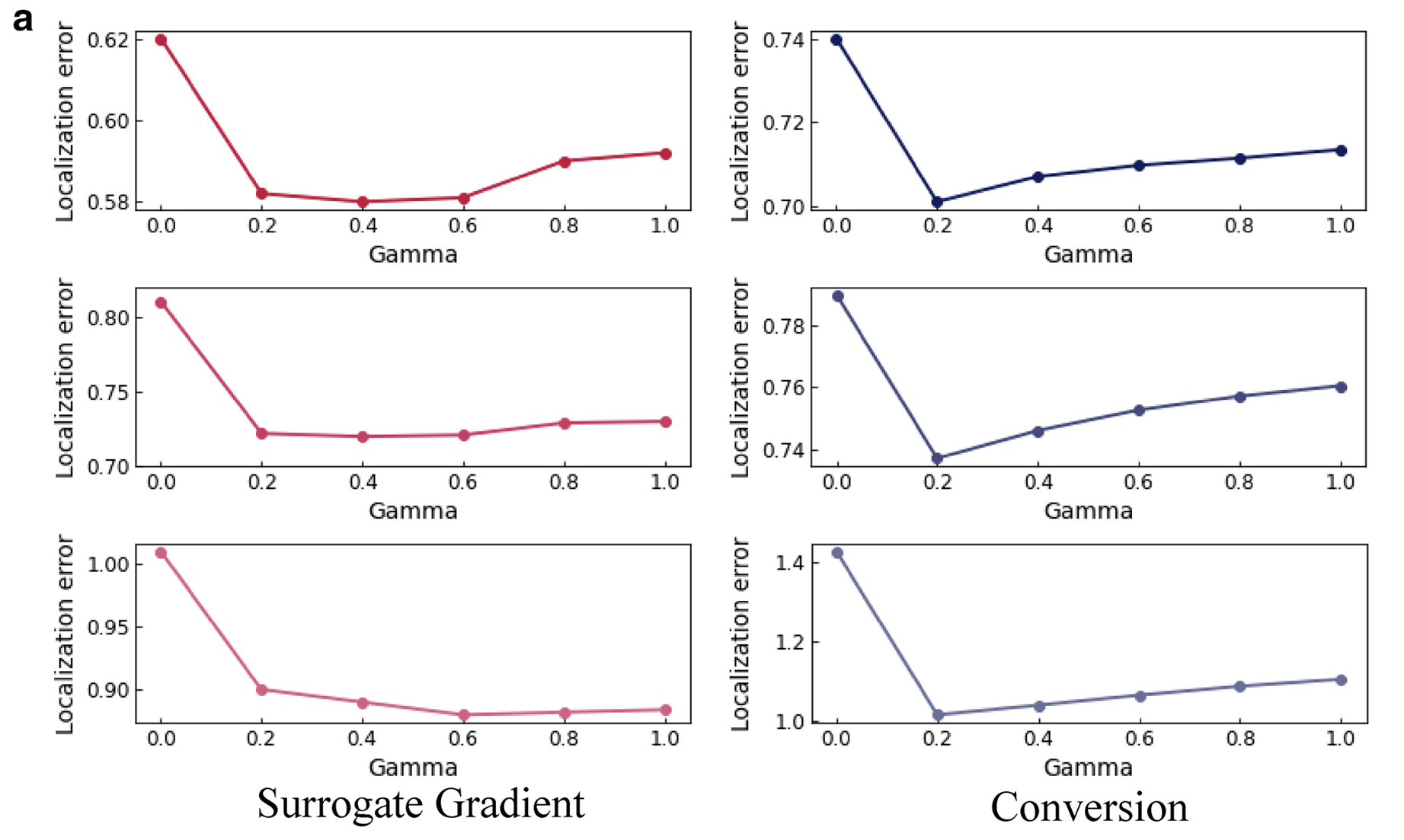
当 $\gamma=0$ 时，定位误差最高，因为此时核函数无法过滤冗余和无关的长 ISI 脉冲。另一个有趣的发现是，当 $\gamma$ 值较大（例如1.0）时，定位误差增加。这是因为高 $\gamma$ 限制了可靠的可视化，仅考虑非常最近的脉冲，并在很大程度上忽略了更长时间的脉冲历史。

对比Direct-training 与 ANNSNN

替代梯度学习的热图可视化呈现出一种趋势：在早期时间步几乎无活动（零活动），随后在中间时间段显示区分性活动，最后在时间末尾又回归零活动。相比之下，转换方法在整个时间周期内保持了类似的热图（如图5b所示）。这种现象与脉冲活动在每个时间步中的变化有关。

很明显，转换方法没有在训练中考虑任何时间动态，这种缺失的时间依赖性导致其可解释性较差。因此，我们认为通过替代梯度学习获得的SNN（结合时间动态）具有更高的可解释性。

SNN 的对抗鲁棒性( Adversarial robustness )

与人类视觉系统不同，神经网络易受到对抗性攻击。这些攻击通过向输入图像添加微小但结构化的扰动来实现。以往研究表明，使用替代梯度训练的 SNN 比 ANN 更能抵抗对抗性输入。为了展示 SNN 在对抗噪声攻击下的有效性，我们进行了 Grad-CAM 和 SAM 的定性与定量比较。

使用快速梯度符号法（FGSM）攻击. 在攻击后，ANN 开始关注图像中的随机区域，从而错误分类对抗性输入。而 SAM 的结果显示，在对抗性攻击情况下，早期时间步的可视化结果相较于干净输入略有变化，但随着时间推移，对抗性输入与干净输入的可视化逐渐趋于一致，高亮显示了适当的兴趣区域。

替代梯度学习因继承了更好的时间动态而更具可解释性，这一观点被广泛接受。同样，人们普遍认为时间动态使 SNN 比 ANN 更能抵抗对抗性攻击。然而，通过 SAM，我们首次使用可视化验证并解释了这一直以来的直觉。由此可见，SAM 是“可解释神经形态计算”的一个入口。

SNN 的感官抑制行为(Sensory suppression behavior)

神经科学研究表明，人类大脑会经历所谓的感官抑制。也就是说，当同时呈现多个对象时，大脑会专注于其中一个对象。巧合的是，通过 SAM，我们观察到 SNN 在呈现多个对象时也模拟了感官抑制行为。