Refs

Energy-Efficient Neuronal Computation via Quantal Synaptic Failures, William B. Levy and Robert A. Baxter; The Journal of Neuroscience, June 1, 2002, 22(11)
Another contribution by synaptic failures to energy e cient processing by neurons, Joanna Tyrcha;∗, William B. Levy; Neurocomputing 58–60 (2004) 59–66

Quantal Synaptic Failures

主要参考Ref.1.

Prior Knowledge 1: Basic Mathematical Modeling of Neurons, a information theory perspective.

🍭Perspective 1: 树突体求和 等价于 香农信道。

随机的突触信号传递过程被视作树突体求和的一部分，而不是像之前视作轴突信息传递。生物学家曾观测到，每一次动作电位的发放导致的神经递质传递是存在一定的故障率的。

在海马体和新皮质中，兴奋性突触占主导地位，且非常不可靠。动作电位达到突触前时引起的量子化神经递质释放的概率约为0.25-0.5（0.25最常见）。
In the hippocampus and in neocortex, excitatory synaptic connections dominate and are remarkably unreliable. Each synapse transmits, at most, a single standardized package called a quantum ( $10^4$ neurotransmitter molecules). When an action potential arrives presynaptically, the probability of evoking the release of one such quantal package is reported to range from 0.25 to 0.5 with 0.5 being less common and 0.25 being quite common (Thomson, 2000), especially when one takes into account the spontaneous rates of neurons (Stevens and Wang, 1994; Destexhe and Pare´, 1999).

关于神经递质释放量子化的解释如下 (~~死去的生理学知识攻击我~~)

神经递质释放的最基本单位是一个突触囊泡的内容物。每个囊泡含有大约相同数目(几千)的递质分子。被释放的递质总量就是这个数的整数倍。因此突触后EPSP的幅度就是对一个囊泡内容物反应幅度的整数倍。换句话说,突触后的EPSP是量子化的,它们是一个量子( quantum)的倍数,反映了在一个突触囊泡的递质分子总数和突触中可用的突触受体的数量。在没有突触前刺激的情况下,许多突触囊泡的胞吐速率极低。这种神经递质自发释放产生的突触后反应可用电生理方法测量。产生的微小反应称为微小突触后电位( miniature postsynaptic potential),通常简称为“mini”。每个mini”是由一个囊泡的递质内容物产生的。因此,由突触前动作电位诱发的EPSP幅度是"mini"幅度的整数倍。

量子突触传递的失败是一种随机过程（Katz, 1966），在生理条件下的存在似乎令人费解。毕竟，如果突触没有利用动作电位，为什么还要费心并耗费资源去传递动作电位？

🍭Perspective 2: 在神经传导过程中，存在故障率 $f$ 和 神经元平均放电率 $p^{\star}$ 的最优状态（最优解），且这个解与神经元数量无关!

当满足

$\begin{equation} f \approx 4^{-\mathcal{H}(p^{\star})} \end{equation}$

时，传递过程是一个最优的。

量子突触失败可以被视为一种相对于神经信息处理所需信息而言的能量效率机制。也就是说，在某些情况下，失败不会降低突触后神经元的计算信息量，但会减少能量消耗和热量生成。

对比两类神经元链接（个人认为可以类比ANN/SNN的中间层和输出层）

特性	en passage systems	boutons terminaux
突触结构	突触分布在轴突的路径上	突触集中在轴突终点
连接目标	通常连接多个突触后神经元	通常连接单一或少量的突触后神经元
传递可靠性	突触传递可能失败，可靠性较低	传递可靠性较高
信号分发	更倾向于信号的广泛分发	更倾向于专一、局部的信号传递
能量消耗	相对较低（通过分散连接减少冗余和能耗）	能量消耗较高，需专注于可靠传输
适用场景	用于广泛分发信号，例如低级调控或大规模感知任务	用于精确传递信号，例如特定动作或感知任务
突触失败的可能性	较高，失败是节能机制的一部分	较低，设计上更注重可靠性

Prior Knowledge 2: Basic Information Theory

Mutual Information (互信息量)

$I(X;Y)\stackrel{def}{=}E_{xy}\biggl[\log\frac{P(XY)}{P(X)P(Y)}\biggr]=H(X)-H(X|Y)=H(Y)-H(Y|X)$

$H(X)\stackrel{def}{=}H(P(X))=-\sum_xP(X)\log P(X)$

$H(X|Y)\overset{def}{\operatorname*{=}}-\sum_yP(Y=y)\sum_xP(X|Y=y)\log P(X|Y=y)$

互信息量的定义是信道容量的最大值，即对于两个通信方 $\mathbf{X}, \mathbf{Y}$ ，使得收发双方的信息熵重叠最大（互信息量最大）的信道是最大容量的。

🍭Perspective 1: 在新皮质神经元轴突中，考虑轴突是个香农信道，那么收发的条件熵 $H(X|Y) = 0$ , 故有 $I(X;Y) = H(X) = H(Y)$

🍭Perspective 2: 在新皮质中，锥体神经元的最大脉冲频率约为 400 Hz，而轴突脉冲的平均频率为 10–20 Hz，远低于仅优化信息传输所需的 200 Hz。

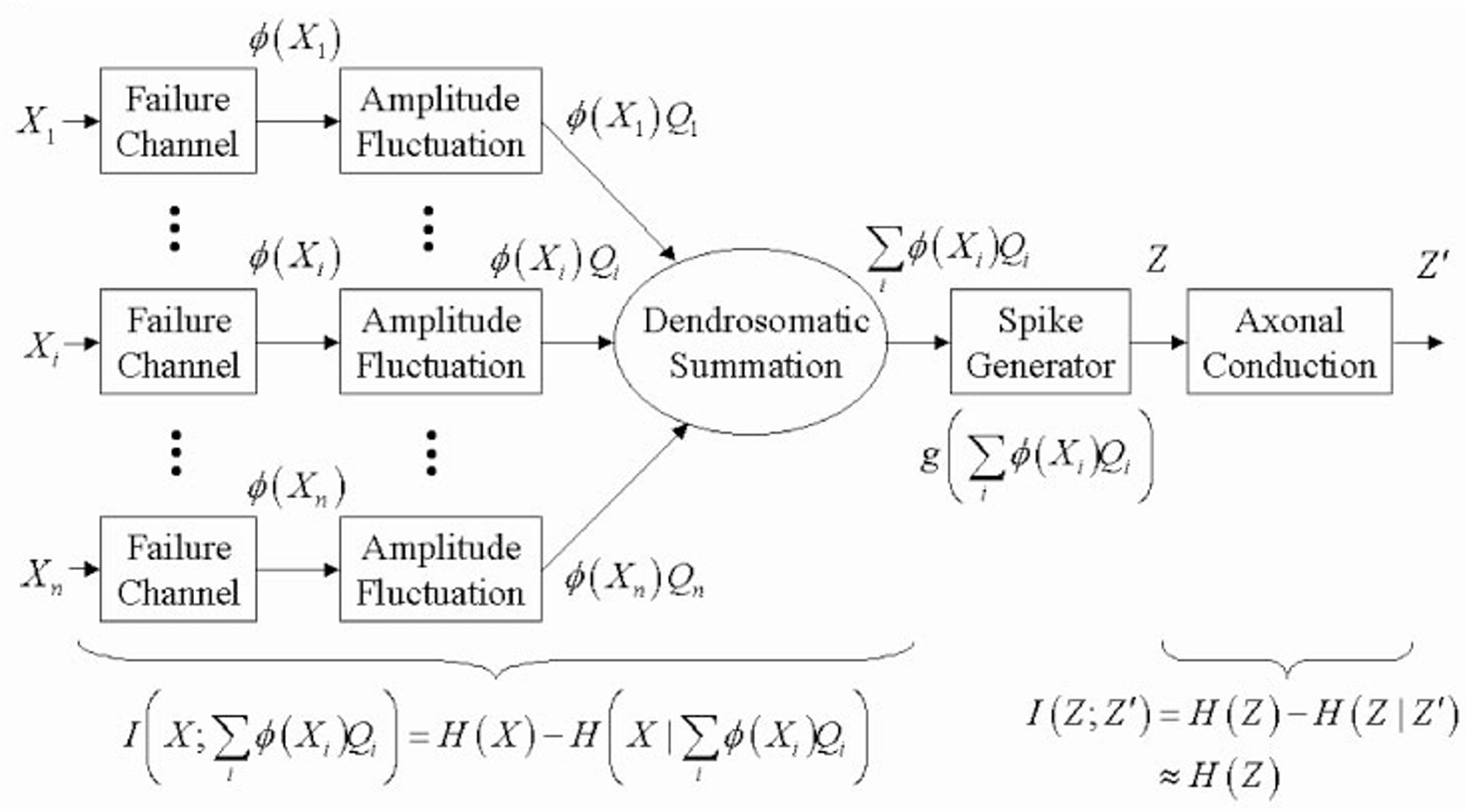
单个神经元的信息流建模

Partitioning communication and computation for a single neuron

The model of failure prone synaptic transmission

引入轴突的能量最优容量的符号，表示为：

$C_E=\max_{P(Z=1)}\left[\frac{H(P(Z))}{\text{轴突能量消耗}}\right]$

符号	注释
$X$	神经元的多元二值输入，表示来自其他神经元的信号输入
$Z$	神经元的输出，是一个单变量二值随机变量，{不发放, 发放} = {0, 1}
$Z'$	神经元输出的传导形式，代表通过轴突传递到突触前的信号
$\phi(X_i)$	第 $i$ 个输入 $X_i$ 的量子释放失败后生成的二值随机变量
$Q_i$	第 $i$ 个输入的量子振幅，在量子释放成功时定义
$f$	量子释放失败的概率， $f = 1 - s$
$s$	量子释放成功的概率， $s = 1 - f$
$H(X)$	输入 $X$ 的信息熵，表示 $X$ 的总信息量
$H(X;{\phi}(X_i)Q_i)$	条件熵，表示在已知 $\phi(X_i)Q_i$ 时 $X$ 的剩余不确定性
$I(X; \phi(X_i)Q_i)$	输入 $X$ 和量子释放后信号之间的互信息
$I(Z; Z')$	神经元输出 $Z$ 和传导信号 $Z'$ 之间的互信息, 由于新皮质轴突的自发脉冲缺乏以及其可靠的传导性，有 $Z=Z'$
$P(Z = 1)$	神经元发放的概率
$C_E$	轴突的能量最优容量，表示单位能量消耗下的最大信息传输量
$p^*$	使轴突容量 $C_E$ 最大化的神经元发放概率

🍭Perspective: 在我们之前的计算（Levy 和 Baxter, 1996）以及来自感知皮层和联络皮层的神经生理学观察中, $p*$ 的范围在 0.025 到 0.05 之间（以 2.5 毫秒为突触驱动锥体神经元的最小发放间隔进行近似）。这对应的 $C_E$ 值在 0.169 到 0.286 比特每 2.5 毫秒之间。

模型假设与信息能量优化的深入探讨

在先前的研究中（Levy和Baxter, 1996）指出，仅在信息容量（或等效的表示容量）这一信号传递信息中，新皮质神经元并未优化信息传递量。在新皮质中，锥体神经元的最大放电频率约为400 Hz，而轴突放电的平均速率为10–20 Hz，而非仅优化信息传递所需的200 Hz。在另一极端，如果一个神经元不存在，就不会有能量消耗，因此单纯从节能的角度看，也未实现最优。然而，将轴突传递信息与能量消耗的比值（一个最终单位bits/J的度量）作为优化目标，得出的最佳放电速率与观察到的放电速率和能量消耗相吻合（Levy和Baxter, 1996）。这一特定优化对后续内容至关重要。

假设脉冲生成器的信息损失可以忽略不计，并且生成额外脉冲的代价也可以忽略。这一假设是由 Attwell 和 Laughlin（2001）的能量审计所支持的。

根据他们的研究，大脑功能中动作电位生成的能量成本主要集中在轴突，占总能量消耗的 47%，这与 Levy 和 Baxter（1996）的结果一致。其次是树突激活的能量消耗，占总能量的 34%。突触传递的预突触部分能量消耗相对较少，而细胞体（因其表面积相对于轴突和树突较小）消耗的能量则可以忽略不计。

假设脉冲生成器是细胞体的一部分，因此生成额外脉冲的能量成本可以忽略，而将脉冲传导到轴突的成本则相对较高。尽管存在这些成本，信息仍必须被传递。

🚩Conjecture: 最大化神经元处理的信息量，并且它的输入信息不会超过它的轴突信道容量。这个信道容量的确定是通过优化信号传输的能效来实现的。

当失败率为零时，计算信息的潜在值可能大于 $H(p)$ ，因为这是一个假设没有噪声的理想状态。然而，由于失败率不为零，这一假设进一步推导出以下结论：失败率的存在可以减少计算的能量消耗，而不会浪费轴突的传输容量。计算信息量被调整到精确等于由能量效率优化定义的传输容量。这种优化机制确保了系统在传输的同时以最小的能量开销达到效率最大化。

考虑一种极端情况: 假设不存在突触失活( $f = 0, \phi(x) = x$ ), $Q_i = 1, s.t. \forall i$ .

$\begin{aligned} I^c = I[X;\sum_{i}\phi(x_i)Q_i] &= H(X) - H(X|\sum_{i}\phi(x_i)Q_i)\\ &=H(X) - H(X|\sum_{i}x_i) \\ &=H(\sum_{i}x_i) - H(\sum_{i}x_i|X)\\ & \leq H(\sum{x_i}) \end{aligned}$

这里我们可以得到该信道的互信息的上确界。再假设X中的每个变量是独立同分布(i.i.d)，那么当 $i \rightarrow +\infty$ ，这个上确界由中心极限定理可知是正态分布的香农熵：

$I^c = \frac{1}{2}\log_2(2\pi e n p^*(1-p^*))$

公式 3 的上确界

假设 $X$ 中的每个变量 $x_i$ 是i.i.d.的随机变量，且 $x_i$ 的成功概率为 $p^*$ 。在这种情况下：

$\sum_{i} x_i$ 是 $n$ 个二项分布变量的和。

根据中心极限定理，当 $n \to \infty$ 时， $\sum_{i} x_i$ 的分布可以近似为正态分布，其均值和方差为：

$\mu = n p^*, \quad \sigma^2 = n p^*(1-p^*)$

对于正态分布 $N(\mu, \sigma^2)$ ，其熵为：

$H(\sum_{i} x_i) = \frac{1}{2} \log_2(2 \pi e \sigma^2)$

代入 $\sigma^2 = n p^*(1-p^*)$ ：

$H(\sum_{i} x_i) = \frac{1}{2} \log_2(2 \pi e n p^*(1-p^*))$

然而，在实际神经网络中，这种独立性假设可能并不完全成立。神经元的输入通常具有一定的统计相关性，但在许多情况下，中心极限定理的结论仍然可以适用，这使得我们能够近似地用正态分布的熵作为上确界。

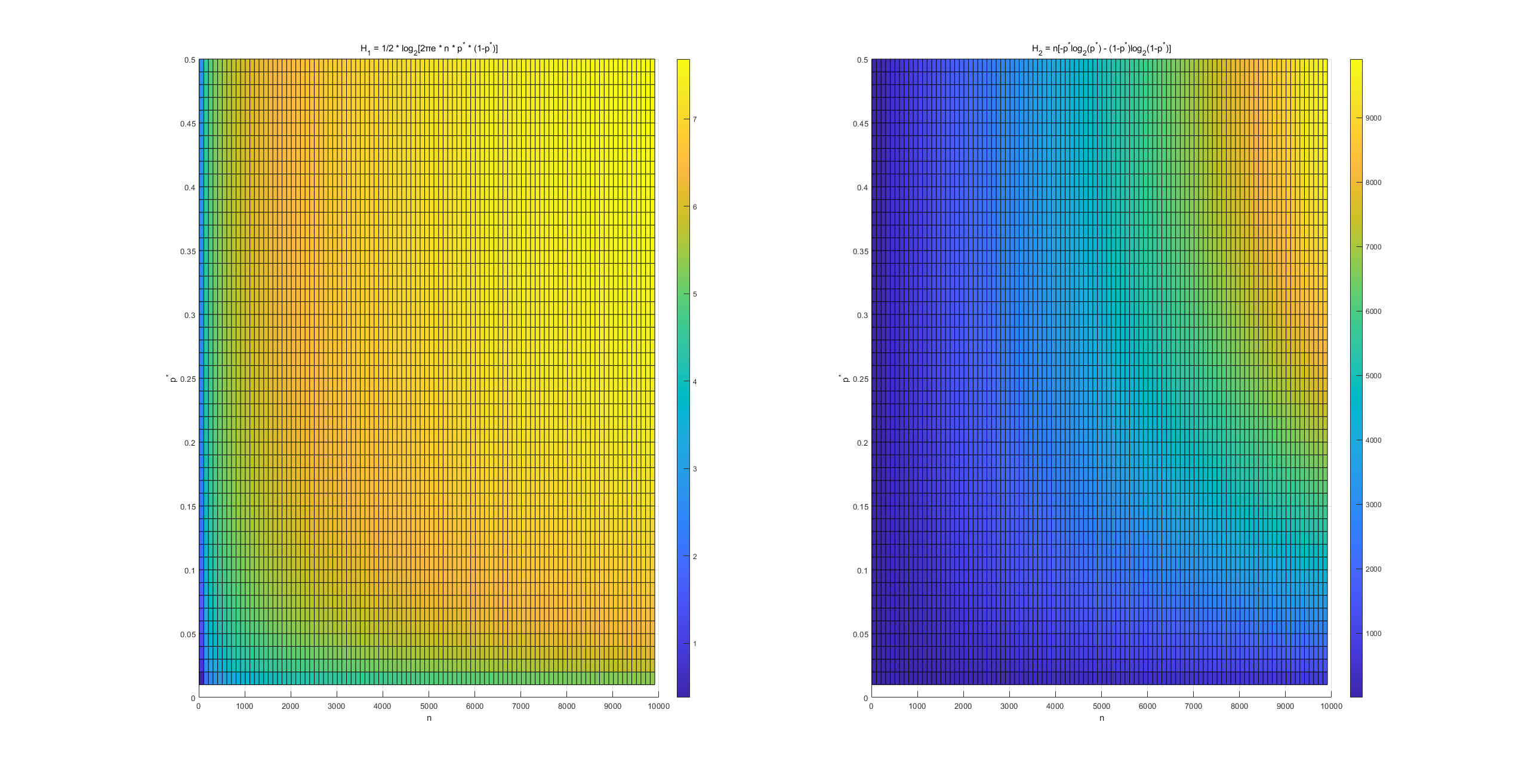
举例：假如 $n=10^4, p^*=0.05$ , $I^C_{upperbound}=6.5$ , 但考虑所有神经元的输入信息量：

$H(X) = n \times H(p^*) = n*[-p^*log_2(p^*) - (1-p)log_2(1-p^*)] = 10000 \times 0.286(bits) = 2860bits$

可视化Matlab代码：

% 定义参数范围
n_values = 10:100:10000; % n 从 10 到 10000，步长为 100
p_values = 0.01:0.01:0.5; % p 从 0.01 到 0.5，步长为 0.01

% 创建网格
[p_grid, n_grid] = meshgrid(p_values, n_values); % 注意这里的顺序！

% 计算公式 H1 和 H2
H1 = 0.5 * log2(2 * pi * exp(1) .* n_grid .* p_grid .* (1 - p_grid));
H2 = n_grid .* (-p_grid .* log2(p_grid) - (1 - p_grid) .* log2(1 - p_grid));

% 将无效的 log2(0) 替换为 0（避免 NaN）
H1(isnan(H1)) = 0;
H2(isnan(H2)) = 0;

% 创建一个图窗
figure;

% 子图 1: H_1
subplot(1, 2, 1); % 1 行 2 列的第 1 个子图
surf(n_grid, p_grid, H1);
xlabel('n');
ylabel('p^*');
zlabel('H_1');
title('H_1 = 1/2 * log_2[2πe * n * p^* * (1-p^*)]');
colormap parula; % 柔和配色
colorbar;

% 子图 2: H_2
subplot(1, 2, 2); % 1 行 2 列的第 2 个子图
surf(n_grid, p_grid, H2);
xlabel('n');
ylabel('p^*');
zlabel('H_2');
title('H_2 = n[-p^*log_2(p^*) - (1-p^*)log_2(1-p^*)]');
colormap parula; % 保持一致配色
colorbar;

Visualization of two information modeling

几个假设

兴奋性神经元的计算是其在每个计算间隔内对输入信号的求和。此类信息处理的互信息可近似表示为：

$I^C=I\left(X ; \sum_i \phi\left(X_i\right) Q_i\right) .$

轴突是二进制信号传输装置，它们在能量最优状态下工作。也就是说，每个轴突在每个计算间隔内以比特速率 $C^E$ 使用，与此对应的尖峰概率为 $p^*$
假设 A2：输入到神经元的输入数量不能过小。例如 $n \gt \frac{2}{p}$ 。显然，在新皮层中，这一条件成立.
在满足假设 A1 和 A2 的前提下，能量更低的过程优于能量更高的过程。
尖峰生成器位于神经元初始段，其将线性树突求和作用上的非线性转化为适合轴突信道的比特级编码。这种编码几乎完美地使用了从树突-胞体计算中获得的信息。

💫很像是编码层啊，很像啊。。。

这一p值来源于Levy和Baxter（1996）的计算结果以及新皮质中观察到的平均放电率。尽管6.5比特与H(X)相比有了极大的下降（在这些假设下，H(X)为2860比特，假设10,000个输入，每个输入为0.286比特），但每个计算间隔6.5比特的信息量相比能量高效的通道容量H(p) = 0.286比特仍是一个非常大的信息量。

基于上述假设的引理

$I^C \leq H(p^*)$ , 即唯一能以能量最优速率 $H(p^*)$ 使用轴突的方法是为其提供至少这么多的信息以供传递。

这个引理的重要性在于以下几点：任何作为计算变换的一部分、能量节约的一部分或计算中干扰波动的一部分的过程都不应该使 $I^C$ 低于 $H(p^*)$ 。特别地，这一引理规定，量子失败作为一种节能装置，只有在 $I^C$ 严格大于 $H(p^*)$ 时才会被使用（或失败率才会增加）。

假设突触兴奋的增加会导致能量消耗单调增加，我们可以认识到要尽可能减少信息传递能耗，就要最大化减少突触激活量（即 $\left.E\left[\sum_i \phi\left(X_i\right) Q_i\right]\right)$ ）。但是，优化过程受到满足信息传递要求的前提下的约束，就是前面提到的四个假设：

假设A2保证神经元的输入数量 $n$ 不能太少。
假设A1保证轴突以能量最优状态运行，这要求平均放电率 $p^*$ 保持不变。
引理1要求信息量 $I^C$ 不能低于轴突容量 $H(p^*)$

结论：实现上述平衡的核心机制。通过适当增加失败率, 达到平衡点即 $I_C=C_E=H\left(p^*\right)$ .（Theorem G.）

Corollary F and its quantified version

随机突触失败的过程可以使神经计算更加节能。

$f \approx\left(\frac{1}{4}\right)^{H\left(p^*\right)}$

固定放电概率，通过调整失败率找到信息传输的平衡点

固定失败率，确定神经元的最佳放电概率

这个结论的一个特点就是，最佳的放电概率与突出随即失活的概率关系与神经元数量 $n$ 无关。通过一个观测到的模型中的神经元脉冲发放概率 $p^*$ , 我们可以唯一确定一个观测范围误差可接受的随机失活概率 $f$ .

DISCUSSION

在以上的所有讨论中，我们是基于一个大前提：假设突触事件是可加的，其次我们假设神经元信号是二进制传递的。如果神经元的活动频率/时间分辨率很高（超过2–104 Hz），则可以通过放电间隔编码（interspike interval coding）来实现比二进制编码更高的能量效率。然而，我们的未发表计算表明，假设放电间隔编码具有极高的时间精度（例如 $10^{-4}ms$ ,其最优放电概率 $p^*$ 可能比二进制编码高50%。然而，我们怀疑这种高时间分辨率的编码仅出现在早期感觉处理和小脑颗粒细胞的输入中。而对于本文研究的系统（例如包含单量子突触、量子失败和10–20 Hz平均放电率的神经元），放电间隔编码将面临明显的限制，因为量子失败可能导致更高的误差率（每次失败产生两个错误），并且观测到的放电率对放电间隔编码来说是次优的，而更适合二进制假设。

本人暂时还没有很理解这一段在说什么…
放电间隔编码划重点

根据公式 $f \approx\left(\frac{1}{4}\right)^{H\left(p^*\right)}$ ，我们能够得出：

最优失败率实际上随着 $p^*$ 增加而减小, 在放电生成器处，放电概率不仅不如物质资源那样“多即贬值”，反而因为二进制熵曲线 $H(p^*)$ 随 $p$ 从0增加到1/2而递增，每个放电和非放电的“价值”实际上变得更高。因此，丢弃一个信号的代价更大。这一结果通过量化分析后才变得清晰，解释了为什么最优失败率是 $p^*$ 的递减函数。
从另一个角度看，限制突触连接( $n$ )的原因可能不在于能量消耗（如本文讨论的），而在于其他因素，例如皮层体积的限制（Mitchison, 1991；Ringo, 1991）或记忆容量的限制（Treves和Rolls, 1992）。

对结论公式的详细推导

Modeling

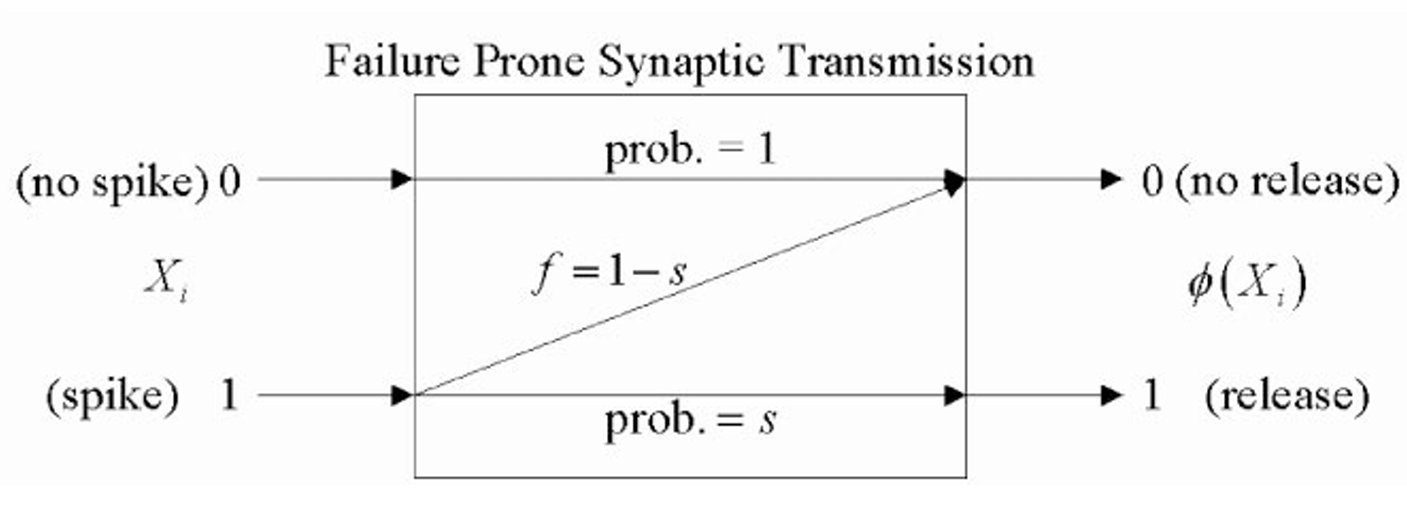
一个神经元接受一个n维的二进制输入向量 $X$ . $X$ 中的每个部分是一个伯努利分布的随机变量，即 $P(X_i=1)=p*$ . 定义 $y = \sum X_i$ 是没有突触失活时随机变量的总和。 $\phi ()$ 是突触失活表征函数，能够作用于每一个输入随机变量： $\phi(X_i)$ , 再定义 $y^{\phi}=\sum \phi(X_i)$ 是存在突触失活时随机变量的总和。量子突触成功传递的比率，是与失活过程互补的，定义为 $P(\phi(X_i)=1|X_i=1) \overset{def}{\operatorname*{=}} s = 1-f$ , 同样的思路考虑如果神经元没有发放脉冲， $P(\phi(X_i)=0|X_i=0)=1$ . 我们研究的对象是 $X$ 和 $\sum \phi(X_i)$ 的互信息量， $I(X;\sum \phi(X_i))$ .

遵循Theorem G:

即当 $I_C=H\left(p^*\right)$ ，

首先，单个突触上的失败通道（failure channel）是独立运行的，与由 $X$ 定义的所有其他输入无关。(换言之， $X$ 这个随机过程中的每个变量 $X_i$ 相互独立). 并且由于总和 $y=\sum X_i$ 对 $X$ 的值进行了划分（partition）(所有可能的 $X$ 值可以根据总和 $y$ 的值划分成不同的集合。), 且 $P\left(\sum \phi\left(X_i\right) \mid X=x\right)=P\left(\sum \phi\left(X_i\right) \mid \sum X_i=y\right)$ (给定 $X$ 的所有输入信号（
或仅给定输入的总和 $y$ 对输出总和 $y^{\phi}$ 的条件概率是等价的。这是基于输入信号独立性以及总和充分统计量的假设。)

所以我们能得到：

$H\left(\sum \phi\left(X_i\right) \mid X\right)=H\left(\sum \phi\left(X_i\right) \mid \sum X_i\right)$

进而得到：

$I\left(X ; \sum \phi\left(X_i\right)\right)=I\left(\sum X_i ; \sum \phi\left(X_i\right)\right)$

如果 $n$ 个独立神经元发生脉冲，且每个的发放概率为 $p$ ，则 $X_i$ 服从二项分布：

$X_i∼Binomial(n,p).$

概率分布函数为：
$P\left(X_i=y \right)=\binom{n}{y} p^k(1-p)^{n-y}$

当满足以下条件时，二项分布会趋近泊松分布：

$n \rightarrow \infty$ ：实验次数趋于无穷；
$p \rightarrow 0$ ：单次实验成功的概率趋近于零;
$n \cdot p=\lambda$ ：实验次数与成功概率的乘积为常数，表示单位时间的平均事件发生次数。

在这种情况下，二项分布的概率公式可以化简为泊松分布的形式

$P(\sum X_i=y)\approx\frac{\lambda^ye^{-\lambda}}{y!}.$

$P(\sum \phi(X_i)=y^{\phi})\approx\frac{\lambda s^{y^{\phi}}e^{-\lambda s}}{y^{\phi}!}.$

量子失败（quantal failure）在每个激活的突触上是独立发生的，这一事实是接下来推导的重要基础。也就是说，某个突触传递失败的概率与其他突触无关，彼此独立。给定输入总数 $y=\sum X_i$ ，总成功数 $y^{\phi} = \sum \phi(X_i)$ 的分布是二项分布(B(y,s))。

$P\left(\sum\phi(X_i)=y^\phi\mid\sum X_i=y\right)=\frac{y!}{(y-y^\phi)! y^\phi!}s^{y^\phi}(1-s)^{y-y^\phi}.$

为了计算 $I(\sum X_i, \sum (\phi(X_i)))$ , 利用：

$I(\sum X_i;\sum\phi(X_i))=H(\sum X_i)-H(\sum X_i|\sum_i\phi(X_i))$

对于参数 $\lambda$ 足够大的泊松分布，可以使用正态分布的近似方法计算熵。泊松分布的熵近似为：

$H\approx\log_2\sqrt{2\pi e\lambda}.$

$I\left(\sum X_i;\sum\phi(X_i)\right)=-\frac12\log_2(1-s)=-\frac12\log_2(f).$

那么，互信息量和能效最优的信道容量满足：

$f = (\frac{1}{4})^{H(p^*)}$

论文后续还讨论了假设泊松分布下的 $Q_i$ 对这个结论的影响，但是实在是看不懂了。。。

Another contribution by synaptic failures to energy efficient processing by neurons

该用Q函数了…

神经元的信道高斯近似。

建模：假设输入之间的多个数据完全独立，服从二项分布。由于输入数量较多，我们可以使用高斯分布来近似二项分布。对于参数为 $n,p$ 的二项分布，期望值 $E(X)=np$ , 方差 $Var(X)=np(1-p)$ . 输入值总和超过阈值（发放脉冲）的概率为：

$P\left(\sum X_{i}>\theta\right)=P\left({\frac{\sum X_{i}-n\,p}{\sqrt{n p(1-p)}}}>{\frac{\theta-n\,p}{\sqrt{n p(1-p)}}}\right)=1-\phi\left({\frac{\theta-n\,p}{\sqrt{n p(1-p)}}}\right)$

其中， $\phi(\cdot)$ 是标准正态分布（standardized normal distribution）的累积分布函数（cumulative distribution function, CDF）。

类比通信原理中的误码率分析

累积分布函数 (CDF) 的定义
累积分布函数描述的是一个随机变量 $X$ 小于或等于某个值 $x$ 的概率。对于一个随机变量 $X$ 其累积分布函数 $F(x)$ 定义为：

$F(x)=P(X\leq x).$

数学上，累积分布函数可以通过概率密度函数 $f(t)$ （PDF, Probability Density Function）积分得到：

$F(x)=\int_{-\infty}^{x}f(t)d t,$

量子突触失败过程对偏度和峰度的影响（Effect of quantal failure process on skewness and kurtosis）

偏度 (Skewness)

统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数值特征：定义为：样本的三阶标准化矩。

$\mathrm{Skewness}=\frac{\mu_{3}}{\sigma^{3}}$

峰度（peakedness、kurtosis）

用来衡量分布曲线的陡峭程度或尾部的厚度的一个指标。它描述了数据在中心峰值附近和尾部的分布情况, 计算方法：随机变量的四阶中心距与方差平方的比值。

$\mathrm{Kurtosis}=\frac{\mu_{4}}{\sigma^{4}}$

高斯分布的偏度为 0，表示完全对称；峰度为 3（或调整后的峰度为 0），表示尾部厚度适中且尖峰适度。
二项分布（遵循参数 $(n,p)$ ）的偏度为 ${\frac{1-2p}{\sqrt{n p(1-p)}}}$ , 峰度为 ${\frac{1-6p(1-p)}{n p(1-p)}}+3.$