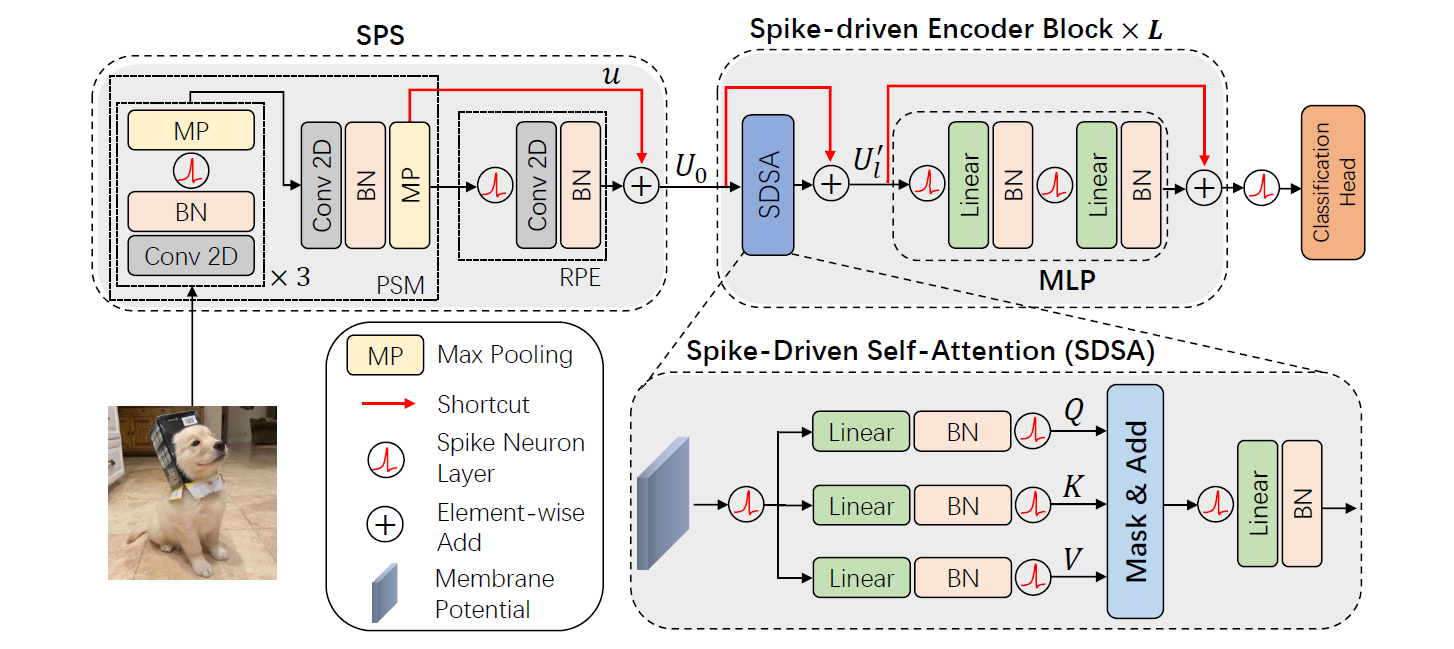
Spike-Driven Transformer
1.注意力机制(Attention)
1.1 自注意力机制 (Self-Attention)
为了处理序列数据,自注意力采取的策略是,吃一整个序列,再根据输入的向量(一段序列)决定输出一个向量,再进入传统的FC,换言之,是考虑了整个序列之后输出一个结果。Self-Attention也可以与FC交替做很多次:
那Self-Attention如何运作?
Self-Attention块的输入可以是一开始的输入层,也可以是中间的某个hidden layer的输出。考虑了所有的输入,输出与输入长度相等的一系列向量。例如考虑了。
以上图为例,怎么产生这个输出呢?
有两种方法,其中Method 1是如今Transformer架构中用到的,也是注意力机制的主流架构,通过点积计算两向量的关联度。
应用中,把一个向量当作query(问询值),其余的所有当作key(键),进行关联度计算,得到Attention Score,再经过Softmax层进行归一化,得到最终的attention-score矩阵。(其实也不一定要softmax,只是前人试出来的)
根据Attention score, 再将每一个向量乘上矩阵得到,
看起来,每一个向量都要产生一个, 那么我们完全可以用矩阵拼接的想法,将一连串的输入向量看作一个大矩阵, 像下面这样简记为:
得到Q,K,V,如何去得到attention score呢?像下面展示的一样,A(attention score的信息矩阵)=
整个的Self-Attention运作的过程中,唯一需要学的三个参数就是
在此基础上,对原始Attention架构更改,得到Multihead Self-Attention:
1.2 Self-Attention的不足之处
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Eric's Blog Site!