refs
Error-backpropagation in temporally encoded networks of spiking neurons, 10.1016/S0925-2312(01)00658-0
Spatio-Temporal Backpropagation for Training High-Performance Spiking Neural Networks, 10.3389/fnins.2018.00331
神经元的脉冲在信息编码中的特点
[29] W. Maass, Fast sigmoidal networks via spiking neurons, Neural Comput. 9 (2) (1997) 279–304.
· 在上述文章中,已经给出证明,脉冲神经网络可以模拟任意形式的前馈sigmoid神经元组成的神经网络。 基于这个特性,SNN可以近似任意的连续函数。SNN中单个尖峰时间传递信息的神经元比具有sigmoid激活函数的神经元计算能力更强。
脉冲 ,在数学上表征为一个“活人/游戏事件”,即“地点,时刻”的坐标。而且活跃(尖峰)神经元的数量通常比较稀少。基于这个特性,SNN可以允许神经网络大模型在VLSI上高效部署。
SNN会产生与Kohonen’s SOM类似的自组织,无监督聚类网
针对时空编码范式的有监督的单脉冲学习算法:基于误差-反向传播的有监督学习算法
概念:阈值函数?(threshold function)
SNN的网络结构
脉冲响应模型:spike response model (SRM),表征输入脉冲和神经元内部的状态的关系。
单个神经元(第j个)的 内在状态(inertial state) 的度量:
x j ( t ) = ∑ i ∈ Γ j w i j ϵ ( t − t i ) x_j(t)=\sum_{i \in \Gamma_j}w_{ij}\epsilon(t-t_i)
x j ( t ) = i ∈ Γ j ∑ w ij ϵ ( t − t i )
式中,w i j w_{ij} w ij
这个式子也表征了一个神经元的未加权的post-synaptic potential(突触后电位)。
至此,我们有了一个基本的认知:神经元的突触前膜产生的若干个电位信号作用在神经元,其和作用达到一个阈值之后,就会产生动作电位,并向下传导 。这和高中学过的神经生理学的知识很相似。
每个突触与前后两个神经元的连接建模如下:
d k =
d_k =
d k =
单个突触末端对神经元状态变量的非加权贡献值为
y i k ( t ) = ϵ ( t − t i − d k ) y_i^k(t) = \epsilon(t-t_i-d^k)
y i k ( t ) = ϵ ( t − t i − d k )
ϵ ( t ) \epsilon(t) ϵ ( t )
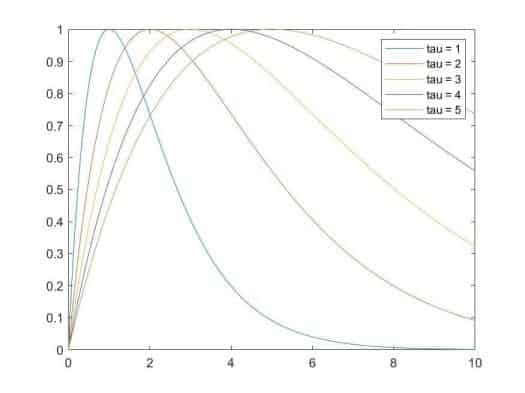
ϵ ( t ) = t τ e 1 − t τ \epsilon(t) = \frac{t}{\tau}e^{1-\frac{t}{\tau}}
ϵ ( t ) = τ t e 1 − τ t
式中τ \tau τ
至此,我们对单个突出的前后电位传递进行了建模。那么重写一下x j ( t ) x_j(t) x j ( t )
x j ( t ) = ∑ i ∈ Γ j ∑ k = 1 m w i j k y i k ( t ) x_j(t) = \sum_{i \in \Gamma_j}\sum_{k=1}^{m} w_{ij}^k y_i^k(t)
x j ( t ) = i ∈ Γ j ∑ k = 1 ∑ m w ij k y i k ( t )
t j t_j t j ϑ \vartheta ϑ
SNN的误差反向传播
假设整个网络包括H(输入层)、I(隐藏层)、J(输出层):
前馈算法的目的是学习一组目标激活时刻/放电时刻(firing times):t j d t_j^d t j d
对于神经元h ∈ H h \in H h ∈ H { P [ t 1 , . . . , t h ] } \{P[t_1, ..., t_h]\} { P [ t 1 , ... , t h ]} j ∈ J j \in J j ∈ J t j a t_j^a t j a
E = 1 2 ∑ j ∈ J ( t j a − t j d ) 2 E = \frac{1}{2}\sum_{j \in J} (t_j^a-t_j^d)^2
E = 2 1 j ∈ J ∑ ( t j a − t j d ) 2
对于误差反向传播,我们将每一个突触连接看作一个单独的作用单元k, 其权重是w i j k w_{ij}^k w ij k
Δ w i j k = − η ∂ E ∂ w i j k \Delta w_{ij}^k = -\eta \frac{\partial E}{\partial w_{ij}^k}
Δ w ij k = − η ∂ w ij k ∂ E
此步就是正常的反向传播 ?思路。η \eta η
∂ E ∂ w i j k = ∂ E ∂ t j ( t j a ) ∂ t j ∂ w i j k ( t j a ) = ∂ E ∂ t j ( t j a ) ∂ t j ∂ x j ( t ) ( t j a ) ∂ x j ( t ) ∂ w i j k ( t j a ) \frac{\partial E}{\partial w_{ij}^k}=\frac{\partial E}{\partial t_j}(t_j^\mathrm{a})\frac{\partial t_j}{\partial w_{ij}^k}(t_j^\mathrm{a})=\frac{\partial E}{\partial t_j}(t_j^\mathrm{a})\frac{\partial t_j}{\partial x_j(t)}(t_j^\mathrm{a})\frac{\partial x_j(t)}{\partial w_{ij}^k}(t_j^\mathrm{a})
∂ w ij k ∂ E = ∂ t j ∂ E ( t j a ) ∂ w ij k ∂ t j ( t j a ) = ∂ t j ∂ E ( t j a ) ∂ x j ( t ) ∂ t j ( t j a ) ∂ w ij k ∂ x j ( t ) ( t j a )
1.
t j t_j t j t = t j a t=t_j^a t = t j a x j ( t ) x_j(t) x j ( t ) t = t j a t=t_j^a t = t j a x j x_j x j
∂ t j ∂ x j ( t ) ( t j a ) = ∂ t j ( x j ) ∂ x j ( t ) ∣ x j = ϑ = − 1 α = − 1 ∂ x j ( t ) / ∂ t ( t j a ) = − 1 ∑ i , l w i j l ( ∂ y i l ( t ) / ∂ t ) ( t j a ) . \left.\frac{\partial t_j}{\partial x_j(t)}(t_j^\mathrm{a})=\left.\frac{\partial t_j(x_j)}{\partial x_j(t)}\right|_{x_j=\vartheta}=\frac{-1}\alpha=\frac{-1}{\partial x_j(t)/\partial t(t_j^\mathrm{a})}=\frac{-1}{\sum_{i,l}w_{ij}^l(\partial y_i^l(t)/\partial t)(t_j^\mathrm{a})}.\right.
∂ x j ( t ) ∂ t j ( t j a ) = ∂ x j ( t ) ∂ t j ( x j ) x j = ϑ = α − 1 = ∂ x j ( t ) / ∂ t ( t j a ) − 1 = ∑ i , l w ij l ( ∂ y i l ( t ) / ∂ t ) ( t j a ) − 1 .
其中,α \alpha α x j ( t ) x_j(t) x j ( t ) t t t x j ( t ) x_j(t) x j ( t ) δ t j \delta t_j δ t j
2.
∂ E ( t j a ) ∂ t j a = ( t j a − t j d ) . \frac{\partial E(t_j^\mathrm{a})}{\partial t_j^\mathrm{a}}=(t_j^\mathrm{a}-t_j^\mathrm{d}).
∂ t j a ∂ E ( t j a ) = ( t j a − t j d ) .
3.
∂ x j ( t j a ) ∂ w i j k = ∂ { ∑ n ∈ Γ j ∑ l w n j l y n l ( t j a ) } ∂ w i j k = y i k ( t j a ) . \frac{\partial x_j(t_j^\mathrm{a})}{\partial w_{ij}^k}=\frac{\partial\{\sum_{n\in\Gamma_j}\sum_lw_{nj}^ly_n^l(t_j^\mathrm{a})\}}{\partial w_{ij}^k}=y_i^k(t_j^\mathrm{a}).
∂ w ij k ∂ x j ( t j a ) = ∂ w ij k ∂ { ∑ n ∈ Γ j ∑ l w nj l y n l ( t j a )} = y i k ( t j a ) .
将上面三个子项代入原始的更新权重中:
Δ w i j k ( t j a ) = − η y i k ( t j a ) ( t j d − t j a ) ∑ i ∈ Γ j ∑ l w i j l ( ∂ y i l ( t j a ) / ∂ t j a ) . \Delta w_{ij}^k(t_j^\mathrm{a})=-\eta\frac{y_i^k(t_j^\mathrm{a})(t_j^\mathrm{d}-t_j^\mathrm{a})}{\sum_{i\in\Gamma_j}\sum_lw_{ij}^l(\partial y_i^l(t_j^\mathrm{a})/\partial t_j^\mathrm{a})}.
Δ w ij k ( t j a ) = − η ∑ i ∈ Γ j ∑ l w ij l ( ∂ y i l ( t j a ) / ∂ t j a ) y i k ( t j a ) ( t j d − t j a ) .
为便于表示,定义超参数δ j \delta_j δ j
δ j ≡ ∂ E ∂ t j a ∂ t j a ∂ x j ( t j a ) = ( t j d − t j a ) ∑ i ∈ Γ j ∑ l w i j l ( ∂ y i l ( t j a ) / ∂ t j a ) \delta_j\equiv\frac{\partial E}{\partial t_j^\mathrm{a}}\mathrm{~}\frac{\partial t_j^\mathrm{a}}{\partial x_j(t_j^\mathrm{a})}=\frac{(t_j^\mathrm{d}-t_j^\mathrm{a})}{\sum_{i\in\Gamma_j}\sum_lw_{ij}^l(\partial y_i^l(t_j^\mathrm{a})/\partial t_j^\mathrm{a})}
δ j ≡ ∂ t j a ∂ E ∂ x j ( t j a ) ∂ t j a = ∑ i ∈ Γ j ∑ l w ij l ( ∂ y i l ( t j a ) / ∂ t j a ) ( t j d − t j a )
Δ w i j k = − η y i k ( t j a ) δ j . \Delta w_{ij}^k=-\eta y_i^k(t_j^\mathrm{a})\delta_j.
Δ w ij k = − η y i k ( t j a ) δ j .
对于第J层之前的隐藏层,同理:对于第i个神经元(i ∈ I i \in I i ∈ I t i a t_i^a t i a
δ i ≡ ∂ t i a ∂ x i ( t i a ) ∂ E ∂ t i a = ∂ t i a ∂ x i ( t i a ) ∑ j ∈ Γ i ∂ E ∂ t j a ∂ t j a ∂ x j ( t j a ) ∂ x j ( t j a ) ∂ t i a = ∂ t i a ∂ x i ( t i a ) ∑ j ∈ Γ i δ j ∂ x j ( t j a ) ∂ t i a , \begin{aligned}
\delta_{i}& \equiv\frac{\partial t_i^\mathbf{a}}{\partial x_i(t_i^\mathbf{a })}\frac{\partial E}{\partial t_i^\mathbf{a}} \\
&=\frac{\partial t_i^\mathrm{a}}{\partial x_i(t_i^\mathrm{a})}\sum_{j\in\Gamma^i}\frac{\partial E}{\partial t_j^\mathrm{a}}\frac{\partial t_j^\mathrm{a}}{\partial x_j(t_j^\mathrm{a})}\frac{\partial x_j(t_j^\mathrm{a})}{\partial t_i^\mathrm{a}} \\
&=\frac{\partial t_i^\mathrm{a}}{\partial x_i(t_i^\mathrm{a})}\sum_{j\in\Gamma^i}\delta_j\frac{\partial x_j(t_j^\mathrm{a})}{\partial t_i^\mathrm{a}},
\end{aligned} δ i ≡ ∂ x i ( t i a ) ∂ t i a ∂ t i a ∂ E = ∂ x i ( t i a ) ∂ t i a j ∈ Γ i ∑ ∂ t j a ∂ E ∂ x j ( t j a ) ∂ t j a ∂ t i a ∂ x j ( t j a ) = ∂ x i ( t i a ) ∂ t i a j ∈ Γ i ∑ δ j ∂ t i a ∂ x j ( t j a ) ,
∂ x j ( t j a ) ∂ t i a = ∂ ∑ l ∈ I ∑ k w l j k y l k ( t j a ) ∂ t i a = ∑ k w i j k ∂ y i k ( t j a ) ∂ t i a . \begin{gathered}
\frac{\partial x_j(t_j^\mathrm{a})}{\partial t_i^\mathrm{a}} =\frac{\partial\sum_{l\in I}\sum_kw_{lj}^ky_l^k(t_j^\mathrm{a})}{\partial t_i^\mathrm{a}} \\
=\sum_kw_{ij}^k\frac{\partial y_i^k(t_j^\mathrm{a})}{\partial t_i^\mathrm{a}}.
\end{gathered} ∂ t i a ∂ x j ( t j a ) = ∂ t i a ∂ ∑ l ∈ I ∑ k w l j k y l k ( t j a ) = k ∑ w ij k ∂ t i a ∂ y i k ( t j a ) .
δ i = ∑ j ∈ Γ i δ j { ∑ k w i j k ( ∂ y i k ( t j a ) / ∂ t i a ) } ∑ h ∈ Γ i ∑ l w h i l ( ∂ y h l ( t i a ) / ∂ t i a ) . \delta_i=\frac{\sum_{j\in\Gamma^i}\delta_j\{\sum_kw_{ij}^k(\partial y_i^k(t_j^\mathrm{a})/\partial t_i^\mathrm{a})\}}{\sum h\in\Gamma_i\sum_lw_{hi}^l(\partial y_h^l(t_i^\mathrm{a})/\partial t_i^\mathrm{a})}.
δ i = ∑ h ∈ Γ i ∑ l w hi l ( ∂ y h l ( t i a ) / ∂ t i a ) ∑ j ∈ Γ i δ j { ∑ k w ij k ( ∂ y i k ( t j a ) / ∂ t i a )} .
Δ w h i k = − η y h k ( t i a ) δ i = − η y h k ( t i a ) ∑ j { δ j ∑ k w i j k ( ∂ y i k ( t j a ) / ∂ t i a ) } ∑ n ∈ Γ i ∑ l w n i l ( ∂ y n l ( t i a ) / ∂ t i a ) . \Delta w_{hi}^k=-\left.\eta y_h^k(t_i^\mathrm{a})\delta_i=-\eta\frac{y_h^k(t_i^\mathrm{a})\sum_j\{\delta_j\sum_kw_{ij}^k(\partial y_i^k(t_j^\mathrm{a})/\partial t_i^\mathrm{a})\}}{\sum_{n\in\Gamma_i}\sum_lw_{ni}^l(\partial y_n^l(t_i^\mathrm{a})/\partial t_i^\mathrm{a})}.\right.
Δ w hi k = − η y h k ( t i a ) δ i = − η ∑ n ∈ Γ i ∑ l w ni l ( ∂ y n l ( t i a ) / ∂ t i a ) y h k ( t i a ) ∑ j { δ j ∑ k w ij k ( ∂ y i k ( t j a ) / ∂ t i a )} .
(以上的所有推导全部基于2002年的误差-反向传播思路,但是太™麻烦,也很难理清思路,不急,有的是时间理清)
tutor:上面的模型有些许误导性,若干个突触连接前后两个神经元,看似是把网络维度扩大了,网络更复杂了。但是如今的SNN网络架构已经摒弃了这种想法。类似ANN,前后神经元仅通过一个权重参数进行前向传播。
我:huh?
error-bp SNN 为什么不好?
SNN发展的几个派系(ε=ε=ε=┏(゜ロ゜;)┛)
ANN-to-SNN:采用近似的思想,实际工程中会造成精度丢失。近似过后的SNN性能也不如ANN。
膜电位驱动的学习算法(membrane potential-driven learning algorithms):空间需求大。
峰值驱动学习算法(spike-driven learning algorithms): 包括SpikeProp 及其衍生算法。这类算法依赖神经元膜电位在点火时间邻域内增长近似线性,导数计算变得更容易。仍存在坏死的神经元 和梯度爆炸 问题(版本答案)
DeepSNN的建模过程以及其训练弊端
考虑一个全连接DeepSNN网络,为便于分析,假设所有神经元最多进行一次点火。V j l V_j^l V j l l l l j j j
V j l ( t ) = ∑ i N ω i j l ε ( t − t i l − 1 ) − η ( t − t j l ) V_j^l(t)=\sum_i^N\omega_{ij}^l\varepsilon\left(t-t_i^{l-1}\right)-\eta(t-t_j^l)
V j l ( t ) = i ∑ N ω ij l ε ( t − t i l − 1 ) − η ( t − t j l )
参数解释:
Parameter
Description
t i l − 1 t_i^{l-1} t i l − 1 第l − 1 l-1 l − 1 i i i
ω i j l \omega_{ij}^l ω ij l 连接神经元N i l − 1 N_i^{l-1} N i l − 1 N j l N_j^{l} N j l
ϵ ( ⋅ ) \epsilon(\cdot) ϵ ( ⋅ ) PSP(突触后电位)函数,以α − \alpha- α −
ϵ ( t − t i l − 1 ) \epsilon(t-t_i^{l-1}) ϵ ( t − t i l − 1 ) 在t i l − 1 t_i^{l-1} t i l − 1
t j l = F { t ∣ V j l ( t ) = ϑ , t ≥ 0 } t_j^l=\mathcal{F}\{t|V_j^l(t)=\vartheta,t\geq0\} t j l = F { t ∣ V j l ( t ) = ϑ , t ≥ 0 } 尖峰发生函数,在膜电位等于ϑ \vartheta ϑ
η ( t − t j l ) \eta(t-t_j^l) η ( t − t j l ) 膜电位恢复函数(refractory kernel)
根据上面对SNN网络的建模,我们可以通过BP算法更新参数:
∂ t j l ∂ ω i j l = ∂ t j l ∂ V j l ( t j l ) ∂ V j l ( t j l ) ∂ ω i j l , i f t j l > t i l − 1 ∂ t j l ∂ t i l − 1 = ∂ t j l ∂ V j l ( t j l ) ∂ V j l ( t j l ) ∂ t i l − 1 , i f t j l > t i l − 1 . \begin{aligned}\frac{\partial t_j^l}{\partial\omega_{ij}^l}&=\frac{\partial t_j^l}{\partial V_j^l\big(t_j^l\big)}\frac{\partial V_j^l\big(t_j^l\big)}{\partial\omega_{ij}^l},&\mathrm{if~}t_j^l>t_i^{l-1}\\\frac{\partial t_j^l}{\partial t_i^{l-1}}&=\frac{\partial t_j^l}{\partial V_j^l\big(t_j^l\big)}\frac{\partial V_j^l\big(t_j^l\big)}{\partial t_i^{l-1}},&\mathrm{if~}t_j^l>t_i^{l-1}.\end{aligned}
∂ ω ij l ∂ t j l ∂ t i l − 1 ∂ t j l = ∂ V j l ( t j l ) ∂ t j l ∂ ω ij l ∂ V j l ( t j l ) , = ∂ V j l ( t j l ) ∂ t j l ∂ t i l − 1 ∂ V j l ( t j l ) , if t j l > t i l − 1 if t j l > t i l − 1 .
计算∂ t j l ∂ V j l ( t j l ) \frac{\partial t_j^l}{\partial V_j^l}(t_j^l) ∂ V j l ∂ t j l ( t j l ) V j l ( t ) V_j^l(t) V j l ( t ) t j t_j t j
∂ t j l ∂ V j l ( t j l ) = − 1 ∂ V j l ( t j l ) / ∂ t j l = − 1 ∑ i N ω i j l ∂ ϵ ( t j l − t i l − 1 ) ∂ t j l \frac{\partial t_j^l}{\partial V_j^l(t_j^l)}=\frac{-1}{\partial V_j^l(t_j^l)/\partial t_j^l}=\frac{-1}{\sum_i^N\omega_{ij}^l\frac{\partial \epsilon\left(t_j^l-t_i^{l-1}\right)}{\partial t_j^l}}
∂ V j l ( t j l ) ∂ t j l = ∂ V j l ( t j l ) / ∂ t j l − 1 = ∑ i N ω ij l ∂ t j l ∂ ϵ ( t j l − t i l − 1 ) − 1
w i t h ∂ ε ( t j l − t i l − 1 ) ∂ t j l = exp ( 1 − ( t j l − t i l − 1 ) / τ ) τ 2 ( τ + t i l − 1 − t j l ) . with\space\frac{\partial\varepsilon\left(t_j^l-t_i^{l-1}\right)}{\partial t_j^l}=\frac{\exp\left(1-\left(t_j^l-t_i^{l-1}\right)/\tau\right)}{\tau^2}\big(\tau+t_i^{l-1}-t_j^l\big).
w i t h ∂ t j l ∂ ε ( t j l − t i l − 1 ) = τ 2 exp ( 1 − ( t j l − t i l − 1 ) / τ ) ( τ + t i l − 1 − t j l ) .
问题一:由于脉冲函数的离散性,脉冲函数不可导
问题二:梯度爆炸发生在∂ V j l ( t j l ) ∂ t j \frac{\partial V_j^l(t_j^l)}{\partial t_j} ∂ t j ∂ V j l ( t j l )
问题三:坏死的神经元(dead neuron):如果突触前电位不足以使神经元点火,即探察不到有t j t_j t j
三个问题怎么克服?
1. ReL-PSP-Based Spiking Neuron Model
索性重新建模神经元:
n e w : V j l ( t ) = ∑ i N ω i j l K ( t − t i l − 1 ) new: \space
V_j^l(t) = \sum_{i}^{N}\omega_{ij}^lK(t-t_i^{l-1})
n e w : V j l ( t ) = i ∑ N ω ij l K ( t − t i l − 1 )
o l d : V j l ( t ) = ∑ i N ω i j l ε ( t − t i l − 1 ) − η ( t − t j l ) old: \space V_j^l(t)=\sum_i^N\omega_{ij}^l\varepsilon\left(t-t_i^{l-1}\right)-\eta(t-t_j^l)
o l d : V j l ( t ) = i ∑ N ω ij l ε ( t − t i l − 1 ) − η ( t − t j l )
对比一下,不难发现,不仅舍去了恢复函数η ( ⋅ ) \eta(\cdot) η ( ⋅ ) ϵ ( ⋅ ) \epsilon(\cdot) ϵ ( ⋅ ) K ( ⋅ ) K(\cdot) K ( ⋅ )
核函数K的定义如下:
K ( t − t i l − 1 ) = { t − t i l − 1 , i f t > t i l − 1 0 , otherwise. K\left(t-t_i^{l-1}\right)=\begin{cases}t-t_i^{l-1},&\mathrm{if~}t>t_i^{l-1}\\0,&\text{otherwise.}&\end{cases}
K ( t − t i l − 1 ) = { t − t i l − 1 , 0 , if t > t i l − 1 otherwise.
眼熟吗?很像一位老朋友:ReLU
R e L U ( x ) = { x , i f x > 0 0 , otherwise. ReLU(x) = \begin{cases}x,&\mathrm{if~}x \gt 0\\0,&\text{otherwise.}&\end{cases}
R e LU ( x ) = { x , 0 , if x > 0 otherwise.
不能说极度相似,简直是一模一样。(难怪作者起这个名字)
ReL-PSP的线性特性,使得膜电位在尖峰时刻达到之前(prior to)线性增长. 计算∂ t j l ∂ V j l ( t j l ) \frac{\partial t_j^l}{\partial V_j^l(t_j^l)} ∂ V j l ( t j l ) ∂ t j l
n e w : ∂ t j l ∂ V j l ( t j l ) = − 1 ∂ V j l ( t j l ) / ∂ t j l = − 1 ∑ i N ω i j l ∂ K ( t j l − t i l − 1 ) ∂ t j l = − 1 ∑ i N ω i j l , i f t j l > t i l − 1 . \begin{aligned}
& new: \space \\
\frac{\partial t_j^l}{\partial V_j^l(t_j^l)}& =-\frac1{\partial V_j^l(t_j^l)/\partial t_j^l} \\
&=\frac{-1}{\sum_i^N\omega_{ij}^l\frac{\partial K\left(t_j^l-t_i^{l-1}\right)}{\partial t_j^l}} \\
&=\frac{-1}{\sum_i^N\omega_{ij}^l},\quad\mathrm{if~}t_j^l>t_i^{l-1}.
\end{aligned}
∂ V j l ( t j l ) ∂ t j l n e w : = − ∂ V j l ( t j l ) / ∂ t j l 1 = ∑ i N ω ij l ∂ t j l ∂ K ( t j l − t i l − 1 ) − 1 = ∑ i N ω ij l − 1 , if t j l > t i l − 1 .
o l d : ∂ t j l ∂ V j l ( t j l ) = − 1 ∂ V j l ( t j l ) / ∂ t j l = − 1 ∑ i N ω i j l ∂ ϵ ( t j l − t i l − 1 ) ∂ t j l old: \space
\frac{\partial t_j^l}{\partial V_j^l(t_j^l)}=\frac{-1}{\partial V_j^l(t_j^l)/\partial t_j^l}=\frac{-1}{\sum_i^N\omega_{ij}^l\frac{\partial \epsilon\left(t_j^l-t_i^{l-1}\right)}{\partial t_j^l}}
o l d : ∂ V j l ( t j l ) ∂ t j l = ∂ V j l ( t j l ) / ∂ t j l − 1 = ∑ i N ω ij l ∂ t j l ∂ ϵ ( t j l − t i l − 1 ) − 1
有了ReL-PSP核函数,我们甚至不用假设近似线性。逐层的累计误差相当于没有了。
梯度爆炸问题中,由于分母中的ω i j l \omega_{ij}
^l ω ij l t j l t_j^l t j l
t j l = ϑ + ∑ i N ω i j l t i l − 1 ∑ i N ω i j l , i f t j l > t i l − 1 . t_j^l=\frac{\vartheta+\sum_i^N\omega_{ij}^lt_i^{l-1}}{\sum_i^N\omega_{ij}^l},\quad\mathrm{if~}t_j^l>t_i^{l-1}.
t j l = ∑ i N ω ij l ϑ + ∑ i N ω ij l t i l − 1 , if t j l > t i l − 1 .
即便是∑ i N ω i j l \sum_{i}^{N}\omega_{ij}^l ∑ i N ω ij l t j l t_j^l t j l N j i N_j^i N j i
(好的这段话已经把我绕晕了)
坏死神经元问题:ReL-PSP摒弃了恢复函数,即膜电位不会恢复,只会不断积累。也就是说无论如何神经元都会发出脉冲,只是时间早晚的问题。
Error-BP
问题背景:n分类问题。
损失函数:交叉熵
L ( g , t o ) = − ln exp ( − t o [ g ] ) ) ∑ i n exp ( − t o [ i ] ) L(g,\mathbf{t^o})=-\ln\frac{\exp(-\mathbf{t^o}[g]))}{\sum_i^n\exp(-\mathbf{t^o}[i])} L ( g , t o ) = − ln ∑ i n exp ( − t o [ i ]) exp ( − t o [ g ]))
输出层函数:softmax
p j = exp ( − t j ) ∑ i n exp ( − t i ) p_j=\frac{\exp(-t_j)}{\sum_i^n\exp(-t_i)}
p j = ∑ i n exp ( − t i ) exp ( − t j )
参数解释:
Parameter
Description
$ \bold {t^o}$
输出层脉冲发射时刻的向量
g g g 目标类别索引
反向传播的偏导计算:
∂ t j l ∂ ω i j l = ∂ t j l ∂ V j l ( t j l ) ∂ V j l ( t j l ) ∂ ω i j l = t i l − 1 − t j l ∑ i N ω i j l , if t j l > t i l − 1 ∂ t j l ∂ t i l − 1 = ∂ t j l ∂ V j l ( t j l ) ∂ V j l ( t j l ) ∂ t i l − 1 = ω i j l ∑ i N ω i j l , if t j l > t i l − 1 . \begin{aligned}\frac{\partial t_j^l}{\partial\omega_{ij}^l}&=\frac{\partial t_j^l}{\partial V_j^l(t_j^l)}\frac{\partial V_j^l(t_j^l)}{\partial\omega_{ij}^l}=\frac{t_i^{l-1}-t_j^l}{\sum_i^N\omega_{ij}^l},&\text{if }t_j^l>t_i^{l-1}\\\frac{\partial t_j^l}{\partial t_i^{l-1}}&=\frac{\partial t_j^l}{\partial V_j^l(t_j^l)}\frac{\partial V_j^l(t_j^l)}{\partial t_i^{l-1}}=\frac{\omega_{ij}^l}{\sum_i^N\omega_{ij}^l},&\text{if }t_j^l>t_i^{l-1}.\end{aligned}
∂ ω ij l ∂ t j l ∂ t i l − 1 ∂ t j l = ∂ V j l ( t j l ) ∂ t j l ∂ ω ij l ∂ V j l ( t j l ) = ∑ i N ω ij l t i l − 1 − t j l , = ∂ V j l ( t j l ) ∂ t j l ∂ t i l − 1 ∂ V j l ( t j l ) = ∑ i N ω ij l ω ij l , if t j l > t i l − 1 if t j l > t i l − 1 .
遗留问题:
为什么反向传播更新的过程中要更新t i l − 1 t_i^{l-1} t i l − 1
关于梯度消失推导的最后一段描述,和坏死神经元的关系?
OpenSMART NoC?
经典算法STBP:
SNN训练的三种方式:
无监督学习:STDP
间接监督学习:ANN-to-SNN
直接监督学习:梯度下降
尖峰神经网络中的迭代泄漏整合与发射模型(Iterative Leaky Integrate-And-Fire (LIF) Model in Spiking Neural Networks)
LIF用于对SNN网络中神经元行为进行描述:
参数解释:
Parameter
Description
u ( t ) u(t) u ( t ) t时刻的神经元膜电位
τ \tau τ 时间常数
I ( t ) I(t) I ( t ) 突触前活动状态,外部刺激和突触权重
V t h V_{th} V t h 膜电位阈值
τ d u ( t ) d t = − u ( t ) + I ( t ) \tau\frac{du(t)}{dt}=-u(t)+I(t)
τ d t d u ( t ) = − u ( t ) + I ( t )
直观感受这个公式,它在描述膜电位随时间的变化状态。变化快慢由τ \tau τ u ( t ) u(t) u ( t ) I ( t ) I(t) I ( t )
为了解决SNN网络在时间域上动态变化复杂,不便于进行反向传播,首先对上述的线性微分方程在u ( t ) ∣ t = t i − 1 u(t) |_{t=t_i-1} u ( t ) ∣ t = t i − 1
u ( t ) = u ( t i − 1 ) e t i − 1 − t τ + I ^ ( t ) u(t) = u(t_{i-1})e^{\frac{t_{i-1}-t}{\tau}} + \hat{I}(t)
u ( t ) = u ( t i − 1 ) e τ t i − 1 − t + I ^ ( t )
即:t时刻的膜电位与前一时刻的膜电位(Temporal Dynamics, TD)以及t时刻突触前输入I ^ ( t ) \hat{I}(t) I ^ ( t )
通过DNN中误差反向传播的训练方法,研究者从中获得启发,DNN的误差反向传播是在空间域上进行的,如何拓展到基于LIF模型的SNN上呢?
x i t + 1 , n = ∑ j = 1 l ( n − 1 ) w i j n o j t + 1 , n − 1 u i t + 1 , n = u i t , n f ( o i t , n ) + x i t + 1 , n + b i n o i t + 1 , n = g ( u i t + 1 , n ) \begin{aligned}
&x_i^{t+1,n} =\sum_{j=1}^{l(n-1)} w_{ij}^no_j^{t+1,n-1} \\
&u_{i}^{t+1,n} =u_i^{t,n}f(o_i^{t,n})+x_i^{t+1,n}+b_i^n \\
&o_{i}^{t+1,n} =g(u_i^{t+1,n})
\end{aligned}
x i t + 1 , n = j = 1 ∑ l ( n − 1 ) w ij n o j t + 1 , n − 1 u i t + 1 , n = u i t , n f ( o i t , n ) + x i t + 1 , n + b i n o i t + 1 , n = g ( u i t + 1 , n )
参数解释:
Parameter
Description
f ( x ) = τ e − x τ f(x) = \tau e^{-\frac{x}{\tau}} f ( x ) = τ e − τ x forget gate(from LSTM ,我去太机智了 ),用于控制TD记忆泄露程度
g ( x ) = { 1 , x ≥ V t h 0 , x < V t h g(x)=\begin{cases}1,&x\ge V_{th}\\0,&x<V_{th}\end{cases} g ( x ) = { 1 , 0 , x ≥ V t h x < V t h output gate(from LSTM),用于控制脉冲释放
上标t
t时刻
n n n 第n层
l ( n ) l(n) l ( n ) (第n层中)第l个神经元
w i j w_{ij} w ij 突触前层第 j 个神经元到突触后层第 i 个神经元的突触权重
o j ∈ { 0 , 1 } o_j \in \{0,1\} o j ∈ { 0 , 1 } 神经元输出脉冲与否,1代表输出,0代表不输出
u i t + 1 , n u_i^{t+1,n} u i t + 1 , n 第n层第i个神经元在t+1时刻的膜电位
x i x_i x i I ^ ( t ) \hat{I}(t) I ^ ( t )
b i b_i b i 表征点火阈值的变量, 利用可调偏置 b 来模拟阈值行为
对于一个很小的时间之内(又要进行必要的假设了),f ( ⋅ ) f(\cdot) f ( ⋅ )
f ( o i t , n ) ≈ { τ , o i t , n = 0 0 , o i t , n = 1 f(o_i^{t,n})\approx\begin{cases}\tau,&o_i^{t,n}=0\\0,&o_i^{t,n}=1\end{cases}
f ( o i t , n ) ≈ { τ , 0 , o i t , n = 0 o i t , n = 1
τ e − 1 τ ≈ 0 \tau e^{-\frac{1}{\tau}} \approx 0 τ e − τ 1 ≈ 0
(额?)
STBP训练框架
定义损失函数为均方误差累积:
L = 1 2 S ∑ s = 1 S ∥ y s − 1 T ∑ t = 1 T o s t , N ∥ 2 2 L=\frac{1}{2S}\sum_{s=1}^{S}\parallel y_s-\frac{1}{T}\sum_{t=1}^{T}\boldsymbol{o}_s^{t,N}\parallel_2^2
L = 2 S 1 s = 1 ∑ S ∥ y s − T 1 t = 1 ∑ T o s t , N ∥ 2 2
参数解释:
Parameter
Description
y s y_s y s 第s个训练样本标签
o s o_s o s 第s个训练样本在特定时刻的输出
损失函数L L L W \boldsymbol{W} W b \boldsymbol{b} b ∂ L ∂ W \frac{\partial L}{\partial \boldsymbol{W}} ∂ W ∂ L ∂ L ∂ b \frac{\partial L}{\partial \boldsymbol{b}} ∂ b ∂ L
假设我们已经得到了每一层n在特定时刻t的输出偏导数:∂ L ∂ o i \frac{\partial L}{\partial o_i} ∂ o i ∂ L ∂ L ∂ u i \frac{\partial L}{\partial u_i} ∂ u i ∂ L
对于单个神经元,传播被分解为垂直路径 SD 和水平路径 TD。SD 中的误差传播数据流类似于 DNN 的典型 BP,即每个神经元累积来自上层的加权误差信号,并迭代更新不同层的参数。而 TD 中的数据流共享相同的神经元状态,这使得直接获得解析解变得相当复杂。为了解决这个问题,研究者利用提出的迭代 LIF 模型 在 SD 和 TD 方向上展开状态空间 ,从而可以区分不同时间步长的 TD 中的状态 ,这就实现了迭代传播的链式规则。Werbos (1990) 中用于训练 RNN 的 BPTT 算法也有类似的思想 。
denote:
δ i t , n = ∂ L ∂ o i t , n \delta_i^{t,n} = \frac{\partial L}{\partial o_i^{t,n}}
δ i t , n = ∂ o i t , n ∂ L
Case 1: t = T t=T t = T n = N n=N n = N
∂ L ∂ o i T , N = − 1 T S ( y i − 1 T ∑ k = 1 T o i k , N ) = δ i T , N . \frac{\partial L}{\partial o_i^{T,N}}=-\frac1{TS}(y_i-\frac1T\sum_{k=1}^To_i^{k,N}) = \delta_i^{T,N}.
∂ o i T , N ∂ L = − TS 1 ( y i − T 1 k = 1 ∑ T o i k , N ) = δ i T , N .
∂ L ∂ u i T , N = ∂ L ∂ o i T , N ∂ o i T , N ∂ u i T , N = δ i T , N ∂ o i T , N ∂ u i T , N . \frac{\partial L}{\partial u_i^{T,N}}=\frac{\partial L}{\partial o_i^{T,N}}\frac{\partial o_i^{T,N}}{\partial u_i^{T,N}}=\delta_i^{T,N}\frac{\partial o_i^{T,N}}{\partial u_i^{T,N}}.
∂ u i T , N ∂ L = ∂ o i T , N ∂ L ∂ u i T , N ∂ o i T , N = δ i T , N ∂ u i T , N ∂ o i T , N .
Case 2: t = T t=T t = T n < N n \lt N n < N
∂ L ∂ o i T , n = ∑ j = 1 l ( n + 1 ) δ j T , n + 1 ∂ o j T , n + 1 ∂ o i T , n = ∑ j = 1 l ( n + 1 ) δ j T , n + 1 ∂ g ∂ u i T , n w j i . \frac{\partial L}{\partial o_i^{T,n}}=\sum_{j=1}^{l(n+1)}\delta_j^{T,n+1}\frac{\partial o_j^{T,n+1}}{\partial o_i^{T,n}}=\sum_{j=1}^{l(n+1)}\delta_j^{T,n+1}\frac{\partial g}{\partial u_i^{T,n}}w_{ji}.
∂ o i T , n ∂ L = j = 1 ∑ l ( n + 1 ) δ j T , n + 1 ∂ o i T , n ∂ o j T , n + 1 = j = 1 ∑ l ( n + 1 ) δ j T , n + 1 ∂ u i T , n ∂ g w ji .
(本人对上式深表怀疑)
∂ L ∂ u i T , n = ∂ L ∂ o i T , n ∂ o i T , n ∂ u i T , n = δ i T , n ∂ g ∂ u i T , n . \frac{\partial L}{\partial u_i^{T,n}}=\frac{\partial L}{\partial o_i^{T,n}}\frac{\partial o_i^{T,n}}{\partial u_i^{T,n}}=\delta_i^{T,n}\frac{\partial g}{\partial u_i^{T,n}}.
∂ u i T , n ∂ L = ∂ o i T , n ∂ L ∂ u i T , n ∂ o i T , n = δ i T , n ∂ u i T , n ∂ g .
Case 3: t < T t \lt T t < T n = N n=N n = N
∂ L ∂ o i t , N = δ i t + 1 , N ∂ o i t + 1 , N ∂ o i t , N + ∂ L ∂ o i T , N = δ i t + 1 , N ∂ g ∂ u i t + 1 , N u i t , N ∂ f ∂ o j t , N + ∂ L ∂ o i T , N , \begin{aligned}
\frac{\partial L}{\partial o_i^{t,N}}& =\delta_i^{t+1,N}\frac{\partial o_i^{t+1,N}}{\partial o_i^{t,N}}+\frac{\partial L}{\partial o_i^{T,N}} \\
&=\delta_i^{t+1,N}\frac{\partial g}{\partial u_i^{t+1,N}}u_i^{t,N}\frac{\partial f}{\partial o_j^{t,N}}+\frac{\partial L}{\partial o_i^{T,N}},
\end{aligned}
∂ o i t , N ∂ L = δ i t + 1 , N ∂ o i t , N ∂ o i t + 1 , N + ∂ o i T , N ∂ L = δ i t + 1 , N ∂ u i t + 1 , N ∂ g u i t , N ∂ o j t , N ∂ f + ∂ o i T , N ∂ L ,
∂ L ∂ u i t , N = ∂ L ∂ u i t + 1 , N ∂ u i t + 1 , N ∂ u i t , N = δ i t + 1 , N ∂ g ∂ u i t + 1 , N f ( o i t , n ) , \frac{\partial L}{\partial u_i^{t,N}}=\frac{\partial L}{\partial u_i^{t+1,N}}\frac{\partial u_i^{t+1,N}}{\partial u_i^{t,N}}=\delta_i^{t+1,N}\frac{\partial g}{\partial u_i^{t+1,N}}f(o_i^{t,n}),
∂ u i t , N ∂ L = ∂ u i t + 1 , N ∂ L ∂ u i t , N ∂ u i t + 1 , N = δ i t + 1 , N ∂ u i t + 1 , N ∂ g f ( o i t , n ) ,
where ∂ L ∂ o i T , N = − 1 T S ( y i − 1 T ∑ k = 1 T o i k , N ) \frac{\partial L}{\partial o_{i}^{T,N}}=-\frac{1}{TS}(y_{i}-\frac{1}{T}\sum_{k=1}^{T}o_{i}^{k,N}) ∂ o i T , N ∂ L = − TS 1 ( y i − T 1 ∑ k = 1 T o i k , N )
Case 4: t < T t \lt T t < T n < N n \lt N n < N
∂ L ∂ o i t , n = ∑ j = 1 l ( n + 1 ) δ j t , n + 1 ∂ o j t , n + 1 ∂ o i t , n + ∂ L ∂ o i t + 1 , n ∂ o i t + 1 , n ∂ o i t , n = ∑ j = 1 l ( n + 1 ) δ j t , n + 1 ∂ g ∂ u i t , n w j i + δ i t + 1 , n ∂ g ∂ u i t , n u i t , n ∂ f ∂ o i t , n , ∂ L ∂ u i t , n = ∂ L ∂ o i t , n ∂ o i t , n ∂ u i t , n + ∂ L ∂ o i t + 1 , n ∂ o i t + 1 , n ∂ u i t , n = δ i t , n ∂ g ∂ u i t , n + δ i t + 1 , n ∂ g ∂ u i t + 1 , n f ( o i t , n ) . \begin{aligned}
&\frac{\partial L}{\partial o_i^{t,n}} =\sum_{j=1}^{l(n+1)}\delta_j^{t,n+1}\frac{\partial o_j^{t,n+1}}{\partial o_i^{t,n}}+\frac{\partial L}{\partial o_i^{t+1,n}}\frac{\partial o_i^{t+1,n}}{\partial o_i^{t,n}} \\
&=\sum_{j=1}^{l(n+1)}\delta_j^{t,n+1}\frac{\partial g}{\partial u_i^{t,n}}w_{ji}+\delta_i^{t+1,n}\frac{\partial g}{\partial u_i^{t,n}}u_i^{t,n}\frac{\partial f}{\partial o_i^{t,n}}, \\
&\frac{\partial L}{\partial u_i^{t,n}} =\frac{\partial L}{\partial o_i^{t,n}}\frac{\partial o_i^{t,n}}{\partial u_i^{t,n}}+\frac{\partial L}{\partial o_i^{t+1,n}}\frac{\partial o_i^{t+1,n}}{\partial u_i^{t,n}} \\
&=\delta_i^{t,n}\frac{\partial g}{\partial u_i^{t,n}}+\delta_i^{t+1,n}\frac{\partial g}{\partial u_i^{t+1,n}}f(o_i^{t,n}).
\end{aligned}
∂ o i t , n ∂ L = j = 1 ∑ l ( n + 1 ) δ j t , n + 1 ∂ o i t , n ∂ o j t , n + 1 + ∂ o i t + 1 , n ∂ L ∂ o i t , n ∂ o i t + 1 , n = j = 1 ∑ l ( n + 1 ) δ j t , n + 1 ∂ u i t , n ∂ g w ji + δ i t + 1 , n ∂ u i t , n ∂ g u i t , n ∂ o i t , n ∂ f , ∂ u i t , n ∂ L = ∂ o i t , n ∂ L ∂ u i t , n ∂ o i t , n + ∂ o i t + 1 , n ∂ L ∂ u i t , n ∂ o i t + 1 , n = δ i t , n ∂ u i t , n ∂ g + δ i t + 1 , n ∂ u i t + 1 , n ∂ g f ( o i t , n ) .
最终得到关于W , b \boldsymbol{W,b} W , b
∂ L ∂ b n = ∑ t = 1 T ∂ L ∂ u t , n ∂ u t , n ∂ b n = ∑ t = 1 T ∂ L ∂ u t , n , \frac{\partial L}{\partial\boldsymbol{b}^n}=\sum_{t=1}^T\frac{\partial L}{\partial\boldsymbol{u}^{t,n}}\frac{\partial\boldsymbol{u}^{t,n}}{\partial \boldsymbol{b}^n}=\sum_{t=1}^T\frac{\partial L}{\partial\boldsymbol{u}^{t,n}},
∂ b n ∂ L = t = 1 ∑ T ∂ u t , n ∂ L ∂ b n ∂ u t , n = t = 1 ∑ T ∂ u t , n ∂ L ,
∂ L ∂ W n = ∑ t = 1 T ∂ L ∂ u t , n ∂ u t , n ∂ W n = ∑ t = 1 T ∂ L ∂ u t , n ∂ u t , n ∂ x t , n ∂ x t , n ∂ W n = ∑ t = 1 T ∂ L ∂ u t , n o t , n − 1 , T , \begin{aligned}
\frac{\partial L}{\partial W^n}& =\sum_{t=1}^T\frac{\partial L}{\partial u^{t,n}}\frac{\partial u^{t,n}}{\partial W^n} \\
&=\sum_{t=1}^T\frac{\partial L}{\partial u^{t,n}}\frac{\partial u^{t,n}}{\partial x^{t,n}}\frac{\partial x^{t,n}}{\partial W^n}=\sum_{t=1}^T\frac{\partial L}{\partial u^{t,n}}o^{t,n-1},T,
\end{aligned}
∂ W n ∂ L = t = 1 ∑ T ∂ u t , n ∂ L ∂ W n ∂ u t , n = t = 1 ∑ T ∂ u t , n ∂ L ∂ x t , n ∂ u t , n ∂ W n ∂ x t , n = t = 1 ∑ T ∂ u t , n ∂ L o t , n − 1 , T ,
(上面这个式子应该是错误的)
对尖峰函数的近似表达:
h 1 ( u ) = 1 a 1 s i g n ( ∣ u − V t h ∣ < a 1 2 ) , h 2 ( u ) = ( a 2 2 − a 2 4 ∣ u − V t h ∣ ) s i g n ( 2 a 2 − ∣ u − V t h ∣ ) , h 3 ( u ) = 1 a 3 e V t h − u a 3 ( 1 + e V t h − u a 3 ) 2 , h 4 ( U ) = 1 2 π a 4 e − ( u − V t h ) 2 2 a 4 , \begin{aligned}
&h_{1}(u) =\frac1{a_1}sign(|u-V_{th}|<\frac{a_1}2), \\
&h_2(u) =(\frac{\sqrt{a_2}}2-\frac{a_2}4|u-V_{th}|)sign(\frac2{\sqrt{a_2}}-|u-V_{th}|), \\
&h_3(u) =\frac1{a_3}\frac{e^{\frac{V_{th}-u}{a_3}}}{(1+e^{\frac{V_{th}-u}{a_3}})^2}, \\
&h_4(\mathcal{U}) =\frac1{\sqrt{2\pi\textit{a}_4}}e^{-\frac{(u-V_{th})^2}{2a_4}},
\end{aligned}
h 1 ( u ) = a 1 1 s i g n ( ∣ u − V t h ∣ < 2 a 1 ) , h 2 ( u ) = ( 2 a 2 − 4 a 2 ∣ u − V t h ∣ ) s i g n ( a 2 2 − ∣ u − V t h ∣ ) , h 3 ( u ) = a 3 1 ( 1 + e a 3 V t h − u ) 2 e a 3 V t h − u , h 4 ( U ) = 2 π a 4 1 e − 2 a 4 ( u − V t h ) 2 ,
STBP代码复现1:MNIST分类任务
ref: https://github.com/yjwu17/STBP-for-training-SpikingNN
a. spiking_model.py
1. 包依赖
1 2 3 import torchimport torch.nn as nnimport torch.nn.functional as F
2. 基本参数设定
1 2 3 4 5 6 7 8 device = torch.device("cuda" if torch.cuda.is_available() else "cpu" ) thresh = 0.5 lens = 0.5 decay = 0.2 num_classes = 10 batch_size = 100 learning_rate = 1e-3 num_epochs = 100
3. 近似点火函数
1 2 3 4 5 6 7 8 9 10 11 12 13 class ActFun (torch.autograd.Function): @staticmethod def forward (ctx, input ): ctx.save_for_backward(input ) return input .gt(thresh).float () @staticmethod def backward (ctx, grad_output ): input , = ctx.saved_tensors grad_input = grad_output.clone() temp = abs (input - thresh) < lens return grad_input * temp.float ()
该部分重写了两个方法:前向传播和反向传播。首先,函数传进torch.autograd.Function,forward 方法接受输入张量 input,将其与预定义的 thresh 进行比较,然后通过 input.gt(thresh).float() 返回一个新的张量,其中每个元素都是对应输入张量元素是否大于阈值的浮点值。ctx.save_for_backward(input) 用于保存输入张量,以便在反向传播时使用。
在反向传播中,backward 方法接受梯度输出 grad_output,然后通过 ctx.saved_tensors 获取保存的输入张量。梯度计算采用了一些条件判断,具体来说,计算了绝对值小于 lens 的部分。最终,返回的梯度是 grad_input * temp.float(),其中 temp 是一个布尔张量,指示输入张量元素是否满足条件。
最后,通过 act_fun = ActFun.apply 创建了一个可以在模型中使用的激活函数。使用时,可以通过调用 act_fun(input) 进行前向传播。
4. 膜电位更新函数
1 2 3 4 def mem_update (ops, x, mem, spike ): mem = mem * decay * (1. - spike) + ops(x) spike = act_fun(mem) return mem, spike
膜电位 * 衰减系数 * (1 - 上一次的脉冲) + 对x运算过后的结果(o p s ( x ) ops(x) o p s ( x )
当前膜电位决定是否点火:a c t _ f u n ( m e n ) act \_ fun(men) a c t _ f u n ( m e n )
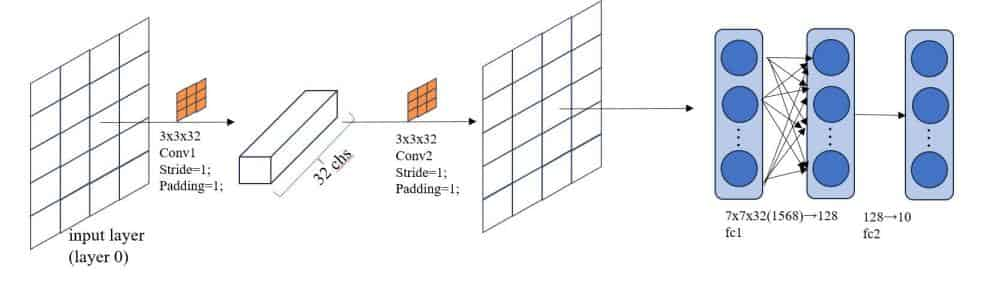
5. CNN网络层配置参数
1 2 3 4 5 6 7 cfg_cnn = [(1 , 32 , 1 , 1 , 3 ), (32 , 32 , 1 , 1 , 3 ), ] cfg_kernel = [28 , 14 , 7 ] cfg_fc = [128 , 10 ]
参数解释:
Parameters
Description
in_planes
输入通道数
out_planes
输出通道数
stride
步长
padding
填充
kernel_size
卷积核大小
第一层:输入通道数为 1,输出通道数为 32,步幅为 1,填充为 1,卷积核大小为 3。
第二层:输入通道数为 32,输出通道数为 32,步幅为 1,填充为 1,卷积核大小为 3。
cfg_kernel: 整数列表,存有不同层次的卷积核大小;
cfg_fc: 整数列表,表示全连接层的配置,一边是128个神经元,一边是10个神经元。
6. 学习率调度器函数
1 2 3 4 5 6 7 def lr_scheduler (optimizer, epoch, init_lr=0.1 , lr_decay_epoch=50 ): """Decay learning rate by a factor of 0.1 every lr_decay_epoch epochs.""" if epoch % lr_decay_epoch == 0 and epoch > 1 : for param_group in optimizer.param_groups: param_group['lr' ] = param_group['lr' ] * 0.1 return optimizer
在每个 lr_decay_epoch 周期后将学习率衰减为原来的 0.1 倍。
optimizer.param_groups是一个包含参数组的列表,每个参数组是一个字典,包含一组参数和这组参数对应的优化选项,如学习率、权重衰减等。
7. SCNN网络架构设计
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class SCNN (nn.Module): def __init__ (self ): super (SCNN, self ).__init__() in_planes, out_planes, stride, padding, kernel_size = cfg_cnn[0 ] self .conv1 = nn.Conv2d(in_planes, out_planes, kernel_size=kernel_size, stride=stride, padding=padding) in_planes, out_planes, stride, padding, kernel_size = cfg_cnn[1 ] self .conv2 = nn.Conv2d(in_planes, out_planes, kernel_size=kernel_size, stride=stride, padding=padding) self .fc1 = nn.Linear(cfg_kernel[-1 ] * cfg_kernel[-1 ] * cfg_cnn[-1 ][1 ], cfg_fc[0 ]) self .fc2 = nn.Linear(cfg_fc[0 ], cfg_fc[1 ]) def forward (self, input , time_window=20 ): c1_mem = c1_spike = torch.zeros(batch_size, cfg_cnn[0 ][1 ], cfg_kernel[0 ], cfg_kernel[0 ], device=device) c2_mem = c2_spike = torch.zeros(batch_size, cfg_cnn[1 ][1 ], cfg_kernel[1 ], cfg_kernel[1 ], device=device) h1_mem = h1_spike = h1_sumspike = torch.zeros(batch_size, cfg_fc[0 ], device=device) h2_mem = h2_spike = h2_sumspike = torch.zeros(batch_size, cfg_fc[1 ], device=device) for step in range (time_window): x = input > torch.rand(input .size(), device=device) c1_mem, c1_spike = mem_update(self .conv1, x.float (), c1_mem, c1_spike) x = F.avg_pool2d(c1_spike, 2 ) c2_mem, c2_spike = mem_update(self .conv2, x, c2_mem, c2_spike) x = F.avg_pool2d(c2_spike, 2 ) x = x.view(batch_size, -1 ) h1_mem, h1_spike = mem_update(self .fc1, x, h1_mem, h1_spike) h1_sumspike += h1_spike h2_mem, h2_spike = mem_update(self .fc2, h1_spike, h2_mem, h2_spike) h2_sumspike += h2_spike outputs = h2_sumspike / time_window return outputs
1. 包依赖
1 2 3 4 5 6 from __future__ import print_functionimport torchvisionimport torchvision.transforms as transformsimport osimport timefrom spiking_model import *
2. 设定训练任务的基本配置
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 names = 'spiking_model' data_path = './MNIST/' device = torch.device("cuda" if torch.cuda.is_available() else "cpu" ) train_dataset = torchvision.datasets.MNIST(root=data_path, train=True , download=True , transform=transforms.ToTensor()) train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True , num_workers=0 ) test_set = torchvision.datasets.MNIST(root=data_path, train=False , download=True , transform=transforms.ToTensor()) test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size, shuffle=False , num_workers=0 ) best_acc = 0 start_epoch = 0 acc_record = list ([]) loss_train_record = list ([]) loss_test_record = list ([]) snn = SCNN() snn.to(device) criterion = nn.MSELoss() optimizer = torch.optim.Adam(snn.parameters(), lr=learning_rate)
3. SCNN训练循环
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 for epoch in range (num_epochs): running_loss = 0 start_time = time.time() for i, (images, labels) in enumerate (train_loader): snn.zero_grad() optimizer.zero_grad() images = images.float ().to(device) outputs = snn(images) labels_ = torch.zeros(batch_size, 10 ).scatter_(1 , labels.view(-1 , 1 ), 1 ) loss = criterion(outputs.cpu(), labels_) running_loss += loss.item() loss.backward() optimizer.step() if (i + 1 ) % 100 == 0 : print ('Epoch [%d/%d], Step [%d/%d], Loss: %.5f' % (epoch + 1 , num_epochs, i + 1 , len (train_dataset) // batch_size, running_loss)) running_loss = 0 print ('Time elapsed:' , time.time() - start_time) correct = 0 total = 0 optimizer = lr_scheduler(optimizer, epoch, learning_rate, 40 )
4. 测试阶段:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 with torch.no_grad(): for batch_idx, (inputs, targets) in enumerate (test_loader): inputs = inputs.to(device) optimizer.zero_grad() outputs = snn(inputs) labels_ = torch.zeros(batch_size, 10 ).scatter_(1 , targets.view(-1 , 1 ), 1 ) loss = criterion(outputs.cpu(), labels_) _, predicted = outputs.cpu().max (1 ) total += float (targets.size(0 )) correct += float (predicted.eq(targets).sum ().item()) if batch_idx % 100 == 0 : acc = 100. * float (correct) / float (total) print (batch_idx, len (test_loader), ' Acc: %.5f' % acc)
5. 输出其他内容和保存模型状态
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 print ('Iters:' , epoch, '\n\n\n' )print ('Test Accuracy of the model on the 10000 test images: %.3f' % (100 * correct / total))acc = 100. * float (correct) / float (total) acc_record.append(acc) if epoch % 5 == 0 : print (acc) print ('Saving..' ) state = { 'net' : snn.state_dict(), 'acc' : acc, 'epoch' : epoch, 'acc_record' : acc_record, } if not os.path.isdir('checkpoint' ): os.mkdir('checkpoint' ) torch.save(state, './checkpoint/ckpt' + names + '.t7' ) best_acc = acc
STBP代码复现2:CIFAR-10分类任务
ref:
Deep Residual Learning in Spiking Neural Networks, Wei Fang et al., Neural Information Processing Systems (NeurIPS) 2021 (SEW/Spike-Element-Wise block)
Differentiable Spike: Rethinking Gradient-Descent for Training Spiking Neural Networks, Yuhang Li et al., Neural Information Processing Systems (NeurIPS 2021). (a new family of Differentiable Spike (Dspike))
1. SEW block的结构:
神经元行为建模:
H [ t ] = f ( V [ t − 1 ] , X [ t ] ) , S [ t ] = Θ ( H [ t ] − V t h ) , V [ t ] = H [ t ] ( 1 − S [ t ] ) + V r e s e t S [ t ] , \begin{aligned}
&H[t] =f(V[t-1],X[t]), \\
&S[t] =\Theta(H[t]-V_{th}), \\
&V[t] =H[t](1-S[t])+V_{reset}S[t],
\end{aligned} H [ t ] = f ( V [ t − 1 ] , X [ t ]) , S [ t ] = Θ ( H [ t ] − V t h ) , V [ t ] = H [ t ] ( 1 − S [ t ]) + V rese t S [ t ] ,
参数解释:
Parameter
Description
H [ t ] H[t] H [ t ] 神经元在进行运算活动之后的膜电位
f ( ⋅ ) f(\cdot) f ( ⋅ ) 神经元动态活动(运算方式),可以是卷积,可以是其他形式
V [ t ] V[t] V [ t ] t时刻发出脉冲之后的膜电位
Θ ( ⋅ ) \Theta(\cdot) Θ ( ⋅ ) 阶跃函数
V t h V_{th} V t h 点火阈值
V r e s e t V_{reset} V rese t 膜电位恢复函数
S [ t ] S[t] S [ t ] t时刻发射的脉冲
例子:两个神经元行为的建模方式:IF(Integrate-and-Fire,式一)和LIF(Leaky-Integrate-and-Fire,式二)
H [ t ] = V [ t − 1 ] + X [ t ] , H [ t ] = V [ t − 1 ] + 1 τ ( X [ t ] − ( V [ t − 1 ] − V r e s e t ) ) , \begin{aligned}&H[t]=V[t-1]+X[t],\\&H[t]=V[t-1]+\frac{1}{\tau}(X[t]-(V[t-1]-V_{reset})),\end{aligned}
H [ t ] = V [ t − 1 ] + X [ t ] , H [ t ] = V [ t − 1 ] + τ 1 ( X [ t ] − ( V [ t − 1 ] − V rese t )) ,
Identity Mapping(恒等映射) : ResNet的核心思想
当F l ( X l ) ≡ 0 , Y l = R e L U ( X l ) \mathcal{F}^l(X^l)\equiv0,Y^l=\mathrm{ReLU(X^l)} F l ( X l ) ≡ 0 , Y l = ReLU ( X l ) X l X^l X l Y l = R e L U ( X l ) = X l Y^l = \mathrm{ReLU(X^l)} = X^l Y l = ReLU ( X l ) = X l
但对于从ANN迁移到SNN的Spiking Resnet块,就无法满足Identity Mapping:
Y l = R e L U ( F l ( X l ) + X l ) , O l [ t ] = S N ( F l ( S l [ t ] ) + S l [ t ] ) . \begin{aligned}Y^l&=\mathrm{ReLU}(\mathcal{F}^l(X^l)+X^l),\\O^l[t]&=\mathrm{SN}(\mathcal{F}^l(S^l[t])+S^l[t]).\end{aligned}
Y l O l [ t ] = ReLU ( F l ( X l ) + X l ) , = SN ( F l ( S l [ t ]) + S l [ t ]) .
当 F l ( S l [ t ] ) ≡ 0 , O l [ t ] = S N ( S l [ t ] ) ≠ S l [ t ] . \mathcal{F}^l(S^l[t])\equiv0,O^{l}[t]=\mathrm{SN}(S^{l}[t])\neq S^{l}[t]. F l ( S l [ t ]) ≡ 0 , O l [ t ] = SN ( S l [ t ]) = S l [ t ] . S N ( S l [ t ] ) = S l [ t ] \mathrm{SN}(S^{l}[t]) = S^{l}[t] SN ( S l [ t ]) = S l [ t ]
mad先不读了,spikingjelly是真好用,文档可视化做的真的不错,非常适合入门
Continue:
对于IF神经元,恒等映射可以满足。设定 0 < V t h ≤ 1 0 \lt V_{th} \leq 1 0 < V t h ≤ 1 V [ t − 1 ] = 0 V[t-1] = 0 V [ t − 1 ] = 0 X [ t ] = 1 X[t] = 1 X [ t ] = 1 H [ t ] > V t h H[t] \gt V_{th} H [ t ] > V t h X [ t ] = 0 X[t] = 0 X [ t ] = 0 H [ t ] < V t h H[t] \lt V_{th} H [ t ] < V t h
但对于更复杂的神经元行为建模方法,很难保证这一条件成立。例如LIF神经元,存在一个电位恢复常数τ \tau τ 0 < V t h ≤ 1 0 \lt V_{th} \leq 1 0 < V t h ≤ 1 V [ t − 1 ] = 0 V[t-1] = 0 V [ t − 1 ] = 0 X [ t ] = 1 X[t] = 1 X [ t ] = 1 H [ t ] = 1 τ H[t] = \frac{1}{\tau} H [ t ] = τ 1 V t h V_{th} V t h
Vanishing & Exploding Gradient in Spiking Resnet blocks
当在t时刻,有k个Spiking Resnet块参与神经网络的前馈传递S l [ t ] S^l[t] S l [ t ]
S l [ t ] = S l + 1 [ t ] = . . . = S l + k − 1 [ t ] = O l + k − 1 [ t ] . S^l[t]=S^{l+1}[t]=...=S^{l+k-1}[t]=O^{l+k-1}[t].
S l [ t ] = S l + 1 [ t ] = ... = S l + k − 1 [ t ] = O l + k − 1 [ t ] .
输出对第l层的输入求偏导进行反向传播时有:
∂ O j l + k − 1 [ t ] ∂ S j l [ t ] = ∏ i = 0 k − 1 ∂ O j l + i [ t ] ∂ S j l + i [ t ] = ∏ i = 0 k − 1 Θ ′ ( S j l + i [ t ] − V t h ) → { 0 , i f 0 < Θ ′ ( S j l [ t ] − V t h ) < 1 1 , i f Θ ′ ( S j l [ t ] − V t h ) = 1 + ∞ , i f Θ ′ ( S j l [ t ] − V t h ) > 1 \frac{\partial O_j^{l+k-1}[t]}{\partial S_j^l[t]}=\prod_{i=0}^{k-1}\frac{\partial O_j^{l+i}[t]}{\partial S_j^{l+i}[t]}=\prod_{i=0}^{k-1}\Theta'(S_j^{l+i}[t]-V_{th})\to\begin{cases}0,\mathrm{if}0<\Theta'(S_j^l[t]-V_{th})<1\\1,\mathrm{if}\Theta'(S_j^l[t]-V_{th})=1\\+\infty,\mathrm{if}\Theta'(S_j^l[t]-V_{th})>1\end{cases}
∂ S j l [ t ] ∂ O j l + k − 1 [ t ] = i = 0 ∏ k − 1 ∂ S j l + i [ t ] ∂ O j l + i [ t ] = i = 0 ∏ k − 1 Θ ′ ( S j l + i [ t ] − V t h ) → ⎩ ⎨ ⎧ 0 , if 0 < Θ ′ ( S j l [ t ] − V t h ) < 1 1 , if Θ ′ ( S j l [ t ] − V t h ) = 1 + ∞ , if Θ ′ ( S j l [ t ] − V t h ) > 1
式中,Θ ( x ) \Theta(x) Θ ( x ) Θ ′ ( x ) \Theta'(x) Θ ′ ( x )
逐元素点火的Resnet块(Spike-Element-Wise Resnet)
O l [ t ] = g ( S N ( F l ( S l [ t ] ) ) , S l [ t ] ) = g ( A l [ t ] , S l [ t ] ) , O^l[t]=g(\mathrm{SN}(\mathcal{F}^l(S^l[t])),S^l[t])=g(A^l[t],S^l[t]),
O l [ t ] = g ( SN ( F l ( S l [ t ])) , S l [ t ]) = g ( A l [ t ] , S l [ t ]) ,
g ( ⋅ ) g(\cdot) g ( ⋅ ) A l [ t ] = S N ( F l ( S l [ t ] ) ) A^l[t] = \mathrm{SN}(\mathcal{F}^l(S^l[t])) A l [ t ] = SN ( F l ( S l [ t ]))
SEW-Resnet的优点:
更易于实现恒等映射:利用尖峰的二进制属性 ,我们可以找到满足恒等映射的不同元素函数g ( ⋅ ) g(\cdot) g ( ⋅ )
Name
Expression of g ( ⋅ ) g(\cdot) g ( ⋅ )
ADD(加)
A l [ t ] + S l [ t ] {A^{l}[t]+S^{l}[t]} A l [ t ] + S l [ t ]
AND(与)
A l [ t ] ∧ S l [ t ] = A l [ t ] ⋅ S l [ t ] \begin{aligned}A^l[t]\wedge S^l[t]=A^l[t]\cdot S^l[t]\end{aligned} A l [ t ] ∧ S l [ t ] = A l [ t ] ⋅ S l [ t ]
IAND
( ¬ A l [ t ] ) ∧ S l [ t ] = ( 1 − A l [ t ] ) ⋅ S l [ t ] (\neg A^l[t])\wedge S^l[t]=(1-A^l[t])\cdot S^l[t] ( ¬ A l [ t ]) ∧ S l [ t ] = ( 1 − A l [ t ]) ⋅ S l [ t ]
e.g.: 选择ADD函数或者IAND函数作为Element-Wise Function,设定A l [ t ] = 0 A^l[t] = 0 A l [ t ] = 0 S N ( F l ( S l [ t ] ) ) = 0 \mathrm{SN}(\mathcal{F}^l(S^l[t])) = 0 SN ( F l ( S l [ t ])) = 0
相反地,选择AND函数,设定A l [ t ] = 1 A^l[t] = 1 A l [ t ] = 1
拓展:SEW-Resnet的下采样块设计:用于输入输出维度不一致的时候。Conv层的步长大于1
SEW-Resnet与ReLU-before-Addition(RBA):
某种程度上,SEW的行为是RBA的行为拓展,但不一样的是,RBA会导致输出层不断积累,而SEW中,使用AND和IAND作为g会输出尖峰(即二元张量),这意味着ANNs中的无限输出问题不会发生在具有SEW块的SNNs中,因为所有尖峰都小于或等于1。当选取ADD为g时,由于k个顺序SEW块的输出不会大于k + 1,可以缓解无穷输出问题。此外,当g为ADD时,一个下采样的SEW块将调节输出不大于2。
SEW对于梯度爆炸/消失问题的缓解
逐层计算( l + k - 1) - th SEW块的输出相对于第l - th SEW块输入的梯度:
∂ O j l + k − 1 [ t ] ∂ S j l [ t ] = ∏ i = 0 k − 1 ∂ g ( A j l + i [ t ] , S j l + i [ t ] ) ∂ S j l + i [ t ] = { ∏ i = 0 k − 1 ∂ ( 0 + S j l + i [ t ] ) ∂ S j l + i [ t ] ,if g = A D D ∏ i = 0 k − 1 ∂ ( 1 ⋅ S j l + i [ t ] ) ∂ S j l + i [ t ] ,if g = A N D ∏ i = 0 k − 1 ∂ ( ( 1 − 0 ) ⋅ S j l + i [ t ] ) ∂ S j l + i [ t ] ,if g = I A N D = 1. \frac{\partial O_j^{l+k-1}[t]}{\partial S_j^l[t]}=\prod_{i=0}^{k-1}\frac{\partial g(A_j^{l+i}[t],S_j^{l+i}[t])}{\partial S_j^{l+i}[t]}=\begin{cases}\prod_{i=0}^{k-1}\frac{\partial(0+S_j^{l+i}[t])}{\partial S_j^{l+i}[t]}\text{,if }g=ADD\\\prod_{i=0}^{k-1}\frac{\partial(1\cdot S_j^{l+i}[t])}{\partial S_j^{l+i}[t]}\text{,if }g=AND\\\prod_{i=0}^{k-1}\frac{\partial((1-0)\cdot S_j^{l+i}[t])}{\partial S_j^{l+i}[t]}\text{,if }g=IAND\end{cases}=1.
∂ S j l [ t ] ∂ O j l + k − 1 [ t ] = i = 0 ∏ k − 1 ∂ S j l + i [ t ] ∂ g ( A j l + i [ t ] , S j l + i [ t ]) = ⎩ ⎨ ⎧ ∏ i = 0 k − 1 ∂ S j l + i [ t ] ∂ ( 0 + S j l + i [ t ]) ,if g = A DD ∏ i = 0 k − 1 ∂ S j l + i [ t ] ∂ ( 1 ⋅ S j l + i [ t ]) ,if g = A N D ∏ i = 0 k − 1 ∂ S j l + i [ t ] ∂ (( 1 − 0 ) ⋅ S j l + i [ t ]) ,if g = I A N D = 1.
补习填坑:复变函数