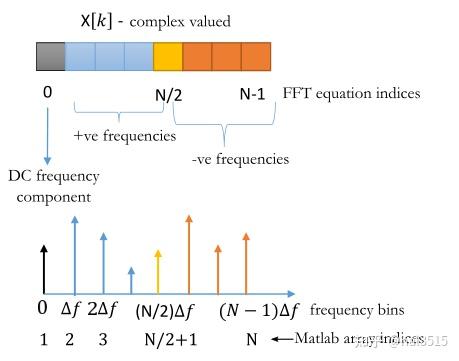
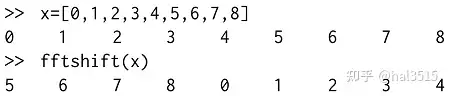Project 1:Matched filtering of Linear Frequency Modulated (LFM) signal 线性调频信号的匹配滤波
FFT function

Parameters:
- sampling time: T
- sampling rate: fs
- $total\ dots: N = T \times f $
- frequency index: △f=Nfs
- original index: N (same as 3.)


Generating Original Waves
s(t)=rect(10×10−6t)ej2π(2×1012t2)
According to the Euler’s formula, we can get:
s(t)=rect(10×10−6t)(cos(2π(2×1012t2))+jsin(2π(2×1012t2)))
The real part of the signal is:
s(t)=rect(10×10−6t)cos(2π(2×1012t2))
The imaginary part of the signal is:
s(t)=rect(10×10−6t)sin(2π(2×1012t2))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| T=10e-6;
B=40e6;
K=B/T;
Fs=2*B;Ts=1/Fs;
N=T/Ts;
t=linspace(-T/2,T/2,N);
St=exp(1i*pi*K*t.^2);
figure(1)
subplot(311)
plot(t*1e6,real(St));
xlabel('time/us');
title('waveform of LFM signal real part');
grid on;axis tight;
subplot(312)
plot(t*1e6,imag(St));
xlabel('time/us');
title('waveform of LFM signal imaginiary part');
grid on;axis tight;
subplot(313)
freq=linspace(-Fs/2,Fs/2,N);
plot(freq*1e-6,fftshift(abs(fft(St))));
xlabel('f/MHz');
title('corresponding amplitude spectrum');
grid on;axis tight;
|
Matched filtering
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| St_wgn = awgn(St,10);
Ht = conj(fliplr(St));
yt = conv(St_wgn, Ht) ;
yf = Sf.*Hf ;
t_0=linspace(-T/2,T/2,2*N-1);
freq=linspace(-Fs/2,Fs/2,2*N-1);
figure(2)
subplot(311)
plot(t_0*1e6,real(yt));
xlabel('time/us');
title('real part of output signal');
grid on;axis tight;
subplot(312)
plot(t_0*1e6,imag(yt));
xlabel('time/us');
title('imaginary part of output signal');
grid on;axis tight;
subplot(313)
plot(freq*1e-6,fftshift(abs(fft(yt))));
xlabel('f/MHz');
title('corresponding amplitude spectrum of output signal');
grid on;axis tight;
|
Principle Analysis
考虑观测信号:$$y(t)=s(t)+n(t)$$
s(t)为已知信号,n(t)为零均值的加性平稳噪声(白色或有色)
令h(t)为滤波器的时不变冲激响应函数,目标就是设计滤波器h(t),使得滤波器的输出信号y(t)的信噪比最大化。
滤波器的输出信号为:
y0(t)=y(t)∗h(t)=∫−∞∞y0(τ)h(t−τ)dτ=∫−∞∞s(τ)h(t−τ)dτ+∫−∞∞n(τ)h(t−τ)dτ=s0(t)+n0(t)
so(t)、no(t)分别为滤波器的输出信号分量和噪声信号分量。
在t=T0时刻,滤波器的输出信噪比定义为
\begin{align}
(\frac{S}{N})^2 & = \frac{\textbf{t=T_0时刻输出的瞬时信号功率}}{\textbf{输出噪声的平均功率}} \\
& = \frac{s_0^2(T_0)}{E[n_0^2(t)]}
\end{align}
利用傅里叶变换的卷积特性,有
s0(t)=∫−∞∞s(τ)h(t−τ)dτ=2π1∫−∞∞H(jω)S(jω)ejωtdω
式中,H(jω) = ∫−∞∞h(t)e−jωtdt为滤波器的频率响应函数(传递函数),S(jω) = ∫−∞∞s(t)e−jωtdt为信号的频谱密度函数。
t=T0时刻,输出信号的瞬时功率为
s02(T0)=∣2π1∫−∞∞H(jω)S(jω)ejωT0dω∣2
t=T0时刻,输出噪声的平均功率为
En02(t)=E{∫−∞∞n(τ)h(t−τ)dτ}2
补一些功率谱密度的知识:
若某一个功率信号x(t)的功率为px(t),则有
px(t)=T→∞lim2T1∣xT(t)∣2
其功率谱密度函数Px(jω)为
Px(jω)=T→∞lim2T1∣XT(jω)∣2
若以f为自变量,则可以写成
Px(f)=T→∞lim2T1∣XT(f)∣2
(其中XT(jω)为xT(t)的傅里叶变换, xT(t)为x(t)在[−T,T]上的截断信号)
根据Parseval定理
∫−∞∞∣xT(t)∣2dt=2π1∫−∞∞∣XT(jω)∣2dω=∫−∞∞∣XT(f)∣2df
总功率为:
P=T→∞lim2T1∫−∞∞∣xT(t)∣2dt=T→∞lim2T1∫−∞∞∣XT(f)∣2df=∫−∞∞P(f)df
令Pn(jω)为加性噪声的功率谱密度函数,则输出噪声的功率谱密度函数为
Pn0(jω)=∣H(jω)∣2Pn(jω)
输出噪声的平均功率可以写作(以频率作为量度)
E[n02(t)]=2π1∫−∞∞Pn0(jω)dω=2π1∫−∞∞∣H(jω)∣2Pn(jω)
代入信噪比定义式,可以得出
(NS)2=E[n02(t)]s02(T0)=2π1∫−∞∞∣H(jω)∣2Pn(jω)∣2π1∫−∞∞H(jω)S(jω)ejωT0dω∣2=2π1∫−∞∞∣H(jω)∣2Pn(jω)∣∫−∞∞(H(jω)Pn(jω))(Pn(jω)S(jω))ejωT0dω∣2
分子凑了一个Pn(jω), 因为要用到Cauchy-Schwartz不等式:
∫abf(x)g(x) dx≤∫abf2(x) dx∫abg2(x) dx
等号在当且仅当f(x)=cg∗(x), c是任意复常数时成立。取c = 1:
f(x)=H(jω)Pn(jω),g(x)=Pn(jω)S(jω)ejωT0
(NS)2≤2π1∫−∞∞∣H(jω)∣2Pn(jω)dω∫−∞∞∣H(jω)∣2Pn(jω)dω∫−∞∞(Pn(jω)∣S(jω)∣2)ejωT0dω=2π1∫−∞∞∣H(jω)∣2Pn(jω)dω∫−∞∞∣H(jω)∣2Pn(jω)dω∫−∞∞(Pn(jω)∣S(jω)∣2)dω=2π1∫−∞∞Pn(jω)∣S(jω)∣2dω
eix的模总是1, 因此平方也是1,复指数乘积项就没了
取最大值,即为等式成立条件。将式中等号成立时的滤波器传递函数记作Hopt(jω), 利用Cauchy-Schwartz不等式等号成立条件:
Hopt(jω)Pn(jω)(cHopt(jω)=Pn∗(jω)S∗(jω)e−jωT0=1)=Pn(jω)S∗(jω)e−jωT0
可以得到最大信噪比:
SNRmax=2π1∫−∞∞Pn(jω)∣S∗(jω)∣2dω
由此,最优线性滤波器理论推导完成。
由题意得其功率谱也恒定为 N2 .代入 Hopt(jω) 中得到:
Hopt(jω)=N2S∗(jω)e−jωT0=2NS∗(jω)e−jωT0
对其进行反变换,得到最优线性滤波器的时域表达式:
hopt(t)=2Ns∗(−t−T0)
T0=0时,最优线性滤波器为:
hopt(t)=2Ns∗(−t)
对应题干中:h(t)=Ks∗(T0−t),T0=0, 能得到N = 2. 该噪声的功率谱密度为1,该噪声为一个白噪声。
Conclusion
- 匹配滤波器的单位冲激响应是原信号的共轭反转信号
- 匹配滤波后的实部输出非常像Sinc Function
原因:输出信号的幅度:
s(t)=rect(Tt)ej2π(2kt2)h(t)=s∗(−t)=rect(T−t)e−j2π(2kt2)s0(t)=s(t)∗h(t)(0≤t≤T)(0≤t≤T)=∫−∞∞h(u)s(t−u)du=∫−∞∞rect(T−u)e−j2π(2ku2)rect(Tt−u)ej2π(2k(t−u)2)du=∫−∞∞rect(T−u)rect(Tt−u)ejπk(t2−2tu)du=∫t−2T2Tejπk(t2−2tu)du=∫t−2T2Tejπkt2e−2jπktudu=ejπkt2∫t−2T2Te−2jπktudu=ejπkt2−2jπkte−2jπktut−2T2T=πktsinπk(T−t)t=πktsinπk(T+t)t
s0(t)=TπkTtsinπkT(1−T∣t∣)trect(2Tt)=TSa(πkTt)rect(2Tt)
当t≤T时,包络近似为辛格(sinc)函数。
- 输出幅度/功率在t=0处有最大值(考虑延迟,则在t=T0)
Radar